题目内容
13.随机调查某社区80个人,以研究这一社区居民在17:00-21:00时间段的休闲方式是否与性别有关,得到下面的数据表:| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
分析 (1)由题意可知,X=0,1,2,3,且每个男性在这一时间段以看书为休闲方式的概率为$P=\frac{10}{30}=\frac{1}{3}$,随机变量X服从二项分布,运用独立重复试验公式求出概率后列出分布列,运用二项分布公式求X的期望;
(2)根据计算出的临界值,同临界值表进行比较,得到有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系.
解答 解:(1)由题意可知,X=0,1,2,3,
且每个男性在这一时间段以看书为休闲方式的概率为$P=\frac{10}{30}=\frac{1}{3}$,
根据题意可得X~B(3,$\frac{1}{3}$),∴$P(X=k)=C_3^k{(\frac{2}{3})^{3-k}}{(\frac{1}{3})^k}$,k=0,1,2,3,
故X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{8}{27}$ | $\frac{4}{9}$ | $\frac{2}{9}$ | $\frac{1}{27}$ |
(2)由${K^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_1}+{n_2}+{n_{+1}}{n_{+2}}}}$,得${K^2}=\frac{{80×{{(45×10-20×5)}^2}}}{65×15×50×30}=\frac{784}{117}≈6.70$,
因为6.70>6.635,所以我们有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系.
点评 本题是一个独立性检验,我们可以利用临界值的大小来决定是否拒绝原来的统计假设,若值较大就拒绝假设,即拒绝两个事件无关.

练习册系列答案
相关题目
1.函数f(x)=2sin(2x+$\frac{π}{3}$+φ)(|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{2}$个单位后关于y轴对称,则以下判断不正确的是( )
| A. | $f({x+\frac{π}{4}})$是奇函数 | B. | $({\frac{π}{4},0})$为f(x)的一个对称中心 | ||
| C. | f(x)在$({-\frac{3π}{4},-\frac{π}{4}})$上单调递增 | D. | f(x)在(0,$\frac{π}{2}$)上单调递减 |
8.若集合A={-1,2},B={0,1},则集合{z|z=x+y,x∈A,y∈B}的子集共有( )
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 16个 |
5.已知数列{an}为等差数列,若a12+a102≤25恒成立,则a1+3a7的取值范围为( )
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
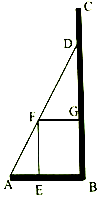 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.