题目内容
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{2x+y≤1}\end{array}\right.$,记z=x+3y的最小值为k,则函数f(x)=ex+k-2的图象恒过定点(2,-1).分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{2x+y≤1}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{2x+y=1}\\{x+y=0}\end{array}\right.$,解得A(1,-1),
化目标函数z=x+3y为y=$-\frac{x}{3}+\frac{z}{3}$,由图可知,当直线y=$-\frac{x}{3}+\frac{z}{3}$过A时,直线在y轴上的截距最小,z有最小值为-2.
∴函数f(x)=ex+k-2=ex-2-2.
取x-2=0,得x=2,f(2)=-1.
故函数f(x)=ex+k-2的图象恒过定点(2,-1).
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
16.已知三条不重合的直线m,n,l和两个不重合的平面α,β,下列命题正确的是( )
| A. | 若m∥n,n?α,则m∥α | B. | 若l∥n,m⊥n,则l∥m | ||
| C. | 若l⊥α,m⊥β,且l⊥m,则α⊥β | D. | 若α⊥β,α∩β=m,且m⊥n,则n⊥α |
13.随机调查某社区80个人,以研究这一社区居民在17:00-21:00时间段的休闲方式是否与性别有关,得到下面的数据表:
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
3.已知抛物线C:y2=16x,焦点为F,直线l:x=-1,点A∈l,线段AF与抛物线C的交点为B,若$\overrightarrow{FA}=5\overrightarrow{FB}$,则|AB|=( )
| A. | $6\sqrt{2}$ | B. | 35 | C. | 28 | D. | 40 |
10.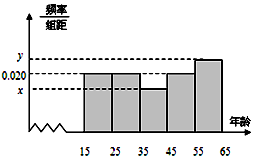 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
| 组号 | 分组 | 喜爱人数 | 喜爱人数占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65) | 20 | 0.80 |