题目内容
4.f(x)=ex-ax2-(a+1)x-1,a∈R,(e为自然对数的底数)(1)a=0时,求f(x)的极值;
(2)若?x0∈[0,1],使得f′(x)≥b成立,求b的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)问题转化为b≤[ex-2ax-(a+1)]max,x∈[0,1],令g(x)=ex-2ax-(a+1),x∈[0,1],求出函数的导数,通过讨论a的范围,求出函数g(x)的最大值,求出b的范围即可.
解答 解:(1)a=0时,f(x)=ex-x,
f′(x)=ex-1,
令f′(x)>0,解得:x>0,
令f′(x)<0,解得:x<0,
故f(x)在(-∞,0)递减,在(0,+∞)递增,
故f(x)极小值=f(0)=1,无极大值;
(2)f′(x)=ex-2ax-(a+1),
若?x0∈[0,1],使得f′(x)≥b成立,
即b≤[ex-2ax-(a+1)]max,x∈[0,1],
令g(x)=ex-2ax-(a+1),x∈[0,1],
g′(x)=ex-2a,
a≤$\frac{1}{2}$时,g′(x)>0,
g(x)在[0,1]递增,g(x)max=g(1)=e-3a-1,
a≥$\frac{e}{2}$时,g′(x)<0,
g(x)在[0,1]递减,g(x)max=g(0)=-a,
$\frac{1}{2}$<a<$\frac{e}{2}$时,令g′(x)>0,解得:x>ln2a,
令g′(x)<0,解得:x<ln2a,
故g(x)在[0,ln2a)递减,在(ln2a,1]递增,
故g(x)max=g(0)或g(1),
综上:b≤$\left\{\begin{array}{l}{e-3a-1,a≤\frac{e-1}{2}}\\{-a,a>\frac{e-1}{2}}\end{array}\right.$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
| A. | ($\frac{l}{6}$)3π | B. | ($\frac{l}{3}$)3π | C. | ($\frac{l}{4}$)3π | D. | $\frac{1}{4}$($\frac{l}{4}$)3π |
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
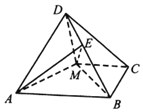 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM. 《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )
《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )