题目内容
11.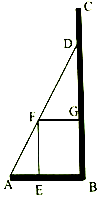 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.(1)试用a,θ表示S1,S2;
(2)若a为定值,BC足够长,当θ为何值时,“规划和谐度”有最小值,最小值是多少?
分析 (1)求出△ABD的面积为,设正方形BEFG的边长为t,利用三角形的相似求出S2,然后求出S1;
(2)由(1)$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1,通过tanθ∈(0,+∞),通过基本不等式推出,当θ=$\frac{π}{4}$时,“规划和谐度”有最小值,最小值是1.
解答 解:(1)∵BD=atanθ,
∴△ABD的面积为$\frac{1}{2}{a}^{2}tanθ$($θ∈(0,\frac{π}{2})$)…(2分)
设正方形BEFG的边长为t,
则由$\frac{FG}{AB}=\frac{DG}{DB}$得$\frac{t}{a}=\frac{atanθ-t}{atanθ}$,∵t=$\frac{atanθ}{1+tanθ}$,…(4分)
∴S2=$\frac{{a}^{2}ta{n}^{2}θ}{(1+tanθ)^{2}}$,
∴S1=$\frac{1}{2}{a}^{2}tanθ$-S2=$\frac{1}{2}{a}^{2}tanθ$-$\frac{{a}^{2}ta{n}^{2}θ}{(1+tanθ)^{2}}$,…(6分)
(2)由(1)$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1,…(8分)
∵tanθ∈(0,+∞),
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{(1+tanθ)^{2}}{2tanθ}$-1=$\frac{1}{2}$(tanθ+$\frac{1}{tanθ}$≥1,…(10分)
当且仅当tanθ=1时取等号,此时θ=$\frac{π}{4}$.
∴当θ=$\frac{π}{4}$时,“规划和谐度”有最小值,最小值是1.…(12分)
点评 本题考查解三角形的实际应用,基本不等式的应用,考查计算能力.

| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
(Ⅱ)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
| A. | 若m∥n,n?α,则m∥α | B. | 若l∥n,m⊥n,则l∥m | ||
| C. | 若l⊥α,m⊥β,且l⊥m,则α⊥β | D. | 若α⊥β,α∩β=m,且m⊥n,则n⊥α |
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?