题目内容
已知F是抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,
•
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是 .
| OA |
| OB |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及
•
=2消元,最后将面积之和表示出来,探求最值问题.
| OA |
| OB |
解答:
解:设直线AB的方程为:x=ty+m,点A(x1,y1),B(x2,y2),直线AB与x轴的交点为M(m,0),
x=ty+m代入y2=x,可得y2-ty-m=0,根据韦达定理有y1•y2=-m,
∵
•
=2,∴x1•x2+y1•y2=2,从而(y1•y2)2+y1•y2-2=0,
∵点A,B位于x轴的两侧,
∴y1•y2=-2,故m=2.
不妨令点A在x轴上方,则y1>0,
又F(
,0),
∴S△ABO+S△AFO=
×2×(y1-y2)+
×
y1=
y1+
≥3
当且仅当
y1=
,即y1=
时,取“=”号,
∴△ABO与△AFO面积之和的最小值是3,
故答案为:3.
x=ty+m代入y2=x,可得y2-ty-m=0,根据韦达定理有y1•y2=-m,
∵
| OA |
| OB |
∵点A,B位于x轴的两侧,
∴y1•y2=-2,故m=2.
不妨令点A在x轴上方,则y1>0,
又F(
| 1 |
| 4 |
∴S△ABO+S△AFO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 9 |
| 8 |
| 2 |
| y1 |
当且仅当
| 9 |
| 8 |
| 2 |
| y1 |
| 4 |
| 3 |
∴△ABO与△AFO面积之和的最小值是3,
故答案为:3.
点评:求解本题时,应考虑以下几个要点:
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知随机变量X服从正态分布N(2,σ2),P(0<X<4)=0.8,则P(X>4)的值等于( )
| A、0.1 | B、0.2 |
| C、0.4 | D、0.6 |
 在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD,PD=AD,AB=2DC,E是PB的中点.求证:
在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD,PD=AD,AB=2DC,E是PB的中点.求证: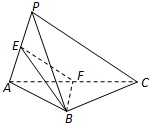 如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;
如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC; 如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为
如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为