题目内容
已知点A(-1,0),点A关于y轴的对称点为B,直线AM,BM相交于点M,且两直线的斜率kAM、kBM满足kAM-kBM=2.
(1)求点M的轨迹C的方程;
(2)设轨迹C与y轴的交点为T,是否存在平行于AT的直线l,使得直线l与轨迹C有公共点,且直线AT与l的距离等于
?若存在,求直线l的方程;若不存在,说明理由.
(1)求点M的轨迹C的方程;
(2)设轨迹C与y轴的交点为T,是否存在平行于AT的直线l,使得直线l与轨迹C有公共点,且直线AT与l的距离等于
| ||
| 2 |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)B(1,0),设M(x,y),则x≠±1,由kAM-kBM=2,得
-
=2,由此能求出点M的轨迹方程.
(2)在方程y=-x2+1中,kAT=1,假设存在符合题意的直线l,其方程为y=x+m,由
,得x2+x+m-1=0,由此求出满足题意的直线l存在,其方程为y=x.
| y |
| x+1 |
| y |
| x-1 |
(2)在方程y=-x2+1中,kAT=1,假设存在符合题意的直线l,其方程为y=x+m,由
|
解答:
解:(1)∵点A(-1,0),点A关于y轴的对称点为B,
∴B(1,0),设M(x,y),则x≠±1,
由kAM-kBM=2,得
-
=2,
整理,得y=-x2+1,
∴点M的轨迹C的方程为y=-x2+1,x≠±1.
(2)在方程y=-x2+1中,令x=0,得y=1,即点T(0,1),
∴kAT=1,
假设存在符合题意的直线l,其方程为y=x+m,
由
,消去y,得x2+x+m-1=0,①
∵直线l与轨迹C有公共点,
∴方程①的根的判别式△=1-4(m-1)≥0,
即m≤
,
又由直线AT与l的距离等于
,得
=
,
解得m=0或m=2,
∵2∉(-∞,
],0∈(-∞,
],
∴满足题意的直线l存在,其方程为y=x.
∴B(1,0),设M(x,y),则x≠±1,
由kAM-kBM=2,得
| y |
| x+1 |
| y |
| x-1 |
整理,得y=-x2+1,
∴点M的轨迹C的方程为y=-x2+1,x≠±1.
(2)在方程y=-x2+1中,令x=0,得y=1,即点T(0,1),
∴kAT=1,
假设存在符合题意的直线l,其方程为y=x+m,
由
|
∵直线l与轨迹C有公共点,
∴方程①的根的判别式△=1-4(m-1)≥0,
即m≤
| 5 |
| 4 |
又由直线AT与l的距离等于
| ||
| 2 |
| |m-1| | ||
|
| ||
| 2 |
解得m=0或m=2,
∵2∉(-∞,
| 5 |
| 4 |
| 5 |
| 4 |
∴满足题意的直线l存在,其方程为y=x.
点评:本题考查点的轨迹方程的求法,考查满足条件的直线方程是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
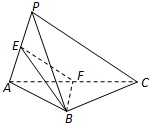 如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;
如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC; 如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为
如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为