题目内容
已知P为椭圆4x2+y2=4上的点,O为原点,则OP的取值范围是 .
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由点P(x,y)在椭圆C上,可得4x2+y2=4,且0≤x2≤1,利用两点间的距离公式将OP表示为x的函数,最后利用二次函数的性质即可求出其范围.
解答:
解:由点P(x,y)在椭圆C上,可得4x2+y2=4,且0≤x2≤1.
OP=
=
因为0≤x2≤1可得1≤4-3x2≤4,所以1≤OP≤2,
故OP的取值范围为[1,2].
故答案为:[1,2].
OP=
| x2+y2 |
| 4-3x2 |
因为0≤x2≤1可得1≤4-3x2≤4,所以1≤OP≤2,
故OP的取值范围为[1,2].
故答案为:[1,2].
点评:本题主要考查了椭圆的标准方程,椭圆的简单性质,考查函数的思想.属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知随机变量X服从正态分布N(2,σ2),P(0<X<4)=0.8,则P(X>4)的值等于( )
| A、0.1 | B、0.2 |
| C、0.4 | D、0.6 |
设a=x3,b=x2-x+1,当x>1时,a与b的大小关系是( )
| A、a<b | B、a=b |
| C、a>b | D、不确定 |
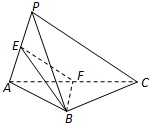 如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;
如图,在三棱锥P-ABC中,PA⊥PC,AB=PB,E,F分别是PA,AC的中点.求证:(1)EF∥平面PBC;