题目内容

已知点A（1，2）在抛物线Γ：y2=2px上．
（1）若△ABC的三个顶点都在抛物线Γ上，记三边AB，BC，CA所在直线的斜率分别为k1，k2，k3，求
1
k1
-
1
k2
+
1
k3
的值；
（2）若四边形ABCD的四个顶点都在抛物线Γ上，记四边AB，BC，CD，DA所在直线的斜率分别为k1，k2，k3，k4，求
1
k1
-
1
k2
+
1
k3
-
1
k4
的值．
考点：直线与圆锥曲线的关系,直线的斜率
专题：圆锥曲线的定义、性质与方程
分析：（1）把点A（1，2）代入抛物线Γ：y2=2px上，可得p=2．即可得到抛物线Γ的方程为：y2=4x．设B(
y
2
1
4
，y1)，C(
y
2
2
4
，y2)．利用斜率计算公式即可得出
1
k1
-
1
k2
+
1
k3
．
（2）设D(
y
2
3
4
，y3)，利用向量计算公式即可得出．
解答： 解：（1）∵点A（1，2）在抛物线Γ：y2=2px上，∴22=2p×1，解得p=2．
∴抛物线Γ的方程为：y2=4x．
设B(
y
2
1
4
，y1)，C(
y
2
2
4
，y2)．
∴k1=
y1-2
y
2
1
4
-1
=
4
y1+2
，k2=
y1-y2
y
2
1
4
-
y
2
2
4
=
4
y1+y2
，k3=
y2-2
y
2
1
4
-1
=
4
y2+2
．
∴
1
k1
-
1
k2
+
1
k3
=
y1+2
4
-
y1+y2
4
+
y2+2
4
=1．
（2）设D(
y
2
3
4
，y3)，
则
1
k1
-
1
k2
+
1
k3
-
1
k4
=
y1+2
4
-
y1+y2
4
+
y2+y3
4
-
y3+2
4
=0．
点评：本题考查了抛物线的标准方程及其性质、斜率计算公式，属于难题．
练习册系列答案
相关题目
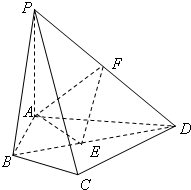如图，四棱锥P-ABCD中，PA⊥面ABCD，E、F分别为BD、PD的中点，EA=EB=AB=1，PA=2．
（Ⅰ）证明：PB∥面AEF；
（Ⅱ）求面PBD与面AEF所成锐角的余弦值．
已知a＞0且a≠1，函数f（x）=ax+a-x（x∈[-1，1]），g（x）=ax2-2ax+4-a（x∈[-1，1]）．
（1）求f（x）的单调区间和值域；
（2）若对于任意x1∈[-1，1]，总存在x0∈[-1，1]，使得g（x0）=f（x1）成立，求a的取值范围；
（3）若对于任意x0∈[-1，1]，任意x1∈[-1，1]，都有g（x0）≥f（x1）恒成立，求a的取值范围．
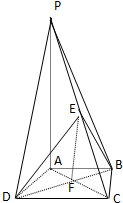如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=2，AD=4，DC=3，PA=5，E∈PC，AC∩BD=F．
（1）若
CE
EP
=
3
2
，求证：EF∥平面PAB；
（2）若FE⊥PC，求二面角E-DB-C的平面角的余弦值．
设
a
=(2cosωx，
3
)，
b
=(sinωx，cos2ωx-sin2ωx)（ω＞0），函数f(x)=
a
•
b
，且函数f（x）图象的一个对称中心与它相邻的一条对称轴之间的距离为
π
4
．
（Ⅰ）求函数f（x）的解析式．
（Ⅱ）在锐角三角形ABC中，角A、B、C的对边分别为a、b、c，且满足f（A）=0，B=
π
4
，a=2，求c边的长．
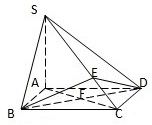已知四棱锥S-ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的任意一点．
（1）求证：平面EBD⊥平面SAC；
（2）当SA=AB时，求二面角B-SC-D的大小．
（1）求函数f(x)=(x-1)0+2
x-1
+
1
3-x
的定义域；
（2）若函数y=f（x）的定义域为[-1，1]，求函数y=f(x+
1
4
)•f(x-
1
4
)的定义域；
（3）求函数y=
x2-x
x2-x+1
的值域．
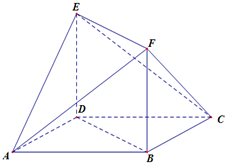如图所示的多面体中，ABCD是菱形，BDEF是矩形，ED⊥平面ABCD，∠BAD=
π
3
，AD=2．
（1）求证：平面FCB∥平面AED；
（2）若二面角A-EF-C为直二面角，求直线BC与平面AEF所成的角θ的正弦值．
已知函数f（x）=x3-3x，若对于任意实数α和β恒有不等式|f（2sinα）-f（2sinβ）|≤
1
m+1
成立，则m的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网