题目内容
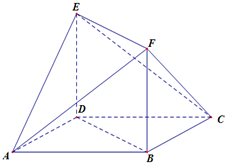 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=| π |
| 3 |
(1)求证:平面FCB∥平面AED;
(2)若二面角A-EF-C为直二面角,求直线BC与平面AEF所成的角θ的正弦值.
考点:与二面角有关的立体几何综合题,平面与平面平行的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明FB∥平面AED,BC∥平面AED,利用面面平行的判定定理可得结论;
(2)取EF的中点M,证明∠AMC就是二面角A-EF-C的平面角.解法1(几何方法):延长CB到G,使BC=BG,证明∠CGM为所求,可得结论;解法2(向量方法):求出平面AEF的法向量,利用向量的夹角公式,即可得出结论.
(2)取EF的中点M,证明∠AMC就是二面角A-EF-C的平面角.解法1(几何方法):延长CB到G,使BC=BG,证明∠CGM为所求,可得结论;解法2(向量方法):求出平面AEF的法向量,利用向量的夹角公式,即可得出结论.
解答:
 (1)证明:矩形BDEF中,FB∥ED,--------(1分)
(1)证明:矩形BDEF中,FB∥ED,--------(1分)
∵FB?平面AED,ED?平面AED,
∴FB∥平面AED,-(2分)
同理BC∥平面AED,-------(3分)
又FB∩BC=B,
∴平面FBC∥平面EDA.------(4分)
(2)解:取EF的中点M.
∵ED⊥面ABCD,ED∥FB,∴ED⊥AD,ED⊥DC,FB⊥BC,FB⊥AB
∵ABCD是菱形,BDEF是矩形,
∴△ADE,△EDC,△ABF,△BCF是全等三角形,
∴AE=AF,CE=CF,
∴AM⊥EF,CM⊥EF,
∴∠AMC就是二面角A-EF-C的平面角-------(8分)
解法1(几何方法):
延长CB到G,使BC=BG,由已知可得,ADBG是平行四边形,又BDEF矩形,
∴AEFG是平行四边形,A,E,F,G共面,
由上证可知,AM⊥MC,CM⊥EF,EF,AM相交于M,
∴CM⊥平面AEFG,
∴∠CGM为所求.

由AD=2,∠DAB=60°,得AC=2
等腰直角三角形AMC中,AC=2
,可得MC=
直角三角形GMC中,sin∠CGM=
=
解法2(向量方法):以D为原点,DC为y轴、DE为z轴,与DC垂直的直线为x轴,建立如图的直角坐标系,由AD=2.则M(
,
,
),C(0,2,0),平面AEF的法向量
=
=(-
,
,-
),-------(12分)

∴
=
=(
,-1,0),
∴cos<
,
>=
=-
,
∴sinθ=
.---(14分)
 (1)证明:矩形BDEF中,FB∥ED,--------(1分)
(1)证明:矩形BDEF中,FB∥ED,--------(1分)∵FB?平面AED,ED?平面AED,
∴FB∥平面AED,-(2分)
同理BC∥平面AED,-------(3分)
又FB∩BC=B,
∴平面FBC∥平面EDA.------(4分)
(2)解:取EF的中点M.
∵ED⊥面ABCD,ED∥FB,∴ED⊥AD,ED⊥DC,FB⊥BC,FB⊥AB
∵ABCD是菱形,BDEF是矩形,
∴△ADE,△EDC,△ABF,△BCF是全等三角形,
∴AE=AF,CE=CF,
∴AM⊥EF,CM⊥EF,
∴∠AMC就是二面角A-EF-C的平面角-------(8分)
解法1(几何方法):
延长CB到G,使BC=BG,由已知可得,ADBG是平行四边形,又BDEF矩形,
∴AEFG是平行四边形,A,E,F,G共面,
由上证可知,AM⊥MC,CM⊥EF,EF,AM相交于M,
∴CM⊥平面AEFG,
∴∠CGM为所求.

由AD=2,∠DAB=60°,得AC=2
| 3 |
等腰直角三角形AMC中,AC=2
| 3 |
| 6 |
直角三角形GMC中,sin∠CGM=
| CM |
| CG |
| ||
| 4 |
解法2(向量方法):以D为原点,DC为y轴、DE为z轴,与DC垂直的直线为x轴,建立如图的直角坐标系,由AD=2.则M(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| n |
| MC |
| ||
| 2 |
| 3 |
| 2 |
| 3 |

∴
| CB |
| DA |
| 3 |
∴cos<
| n |
| CB |
| ||||
|
|
| ||
| 4 |
∴sinθ=
| ||
| 4 |
点评:本题考查线面平行、面面平行,考查线面角,考查学生分析解决问题的能力,正确找出线面角是关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
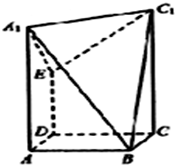 在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E
在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E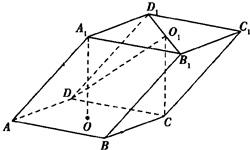 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.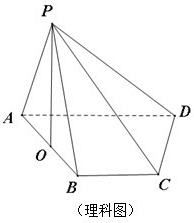 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.