题目内容
已知函数f(x)=x3-3x,若对于任意实数α和β恒有不等式|f(2sinα)-f(2sinβ)|≤
成立,则m的取值范围是 .
| 1 |
| m+1 |
考点:利用导数求闭区间上函数的最值,函数恒成立问题
专题:函数的性质及应用
分析:将不等式恒成立转化为求|f(x)max-f(x)min|≤
,即可得到结论.
| 1 |
| m+1 |
解答:
解:|f(2sinα)-f(2sinβ)|≤m恒成立,
等价于|f(x)max-f(x)min|≤
,
由于2sinα∈[-2,2],2sinβ∈[-2,2],
故只需求出f(x)=x3-3x在[-2,2]上的最值,
而f′(x)=3x2-3,
由f′(x)=0得x=±1
列表如下:
∴f(x)max=2,f(x)min=-2,
∴|f(x)max-f(x)min|=4,
即4≤
,
∴0<m+1≤
,
即-1<m≤-
∴m的取值范围是(-1,-
],
故答案为:(-1,-
].
等价于|f(x)max-f(x)min|≤
| 1 |
| m+1 |
由于2sinα∈[-2,2],2sinβ∈[-2,2],
故只需求出f(x)=x3-3x在[-2,2]上的最值,
而f′(x)=3x2-3,
由f′(x)=0得x=±1
列表如下:
| x | -2 | (-2,-1) | -1 | (-1,1) | 1 | (1,2) | 2 |
| f'(x) | + | - | + | ||||
| f(x) | -2 | 递增 | 2 | 递减 | -2 | 递增 | 2 |
∴|f(x)max-f(x)min|=4,
即4≤
| 1 |
| m+1 |
∴0<m+1≤
| 1 |
| 4 |
即-1<m≤-
| 3 |
| 4 |
∴m的取值范围是(-1,-
| 3 |
| 4 |
故答案为:(-1,-
| 3 |
| 4 |
点评:本题主要考查利用导数求函数的最值问题,利用不等式恒成立的等价条件,将条件转化为求|f(x)max-f(x)min|≤
是解决本题的关键.
| 1 |
| m+1 |

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知命题p:-4<x-a<4,命题q:(x-1)(x-3)<0,且q是p的充分而不必要条件,则a的取值范围是( )
| A、[-1,5] |
| B、[-1,5) |
| C、(-1,5] |
| D、(-1,5) |
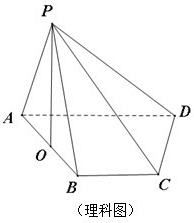 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.