题目内容
已知a>0且a≠1,函数f(x)=ax+a-x(x∈[-1,1]),g(x)=ax2-2ax+4-a(x∈[-1,1]).
(1)求f(x)的单调区间和值域;
(2)若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,求a的取值范围;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,求a的取值范围.
(1)求f(x)的单调区间和值域;
(2)若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,求a的取值范围;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,求a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)先判断函数的奇偶性,然后根据复合函数单调性之间的关系,即可求f(x)的单调区间和值域;
(2)若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,即等价于g(x)max≥f(x)max且g(x)min≥f(x)min,然后可a的取值范围;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,等价为g(x)min≥f(x)max,即可求a的取值范围.
(2)若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,即等价于g(x)max≥f(x)max且g(x)min≥f(x)min,然后可a的取值范围;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,等价为g(x)min≥f(x)max,即可求a的取值范围.
解答:
解:(1)∵f(x)=ax+a-x(x∈[-1,1]),
则f(-x)=ax+a-x=f(x),为偶函数,
设t=ax,则函数f(x)等价为y=t+
,
若a>1,当0≤x≤1时,t=ax单调递增,且t≥1,此时函数y=t+
在t≥1上单调递增,∴根据复合函数的单调性可知此时f(x)单调递增.
若0<a<1,当0≤x≤1时,t=ax单调递减,且0<t≤1,此时函数y=t+
在0<t≤1上单调递减,∴根据复合函数的单调性可知此时f(x)单调递增.
综上当x≥0时,函数单调递增,
∵函数f(x)是偶函数,∴当-1≤x≤0时,函数单调递减.
故函数的递增区间为[0,1],递减区间为[-1,0].
∴函数的值域为[2,a+
].
(2)∵a>0且a≠1,
∴g(x)=ax2-2ax+4-a(x∈[-1,1])的对称轴为x=-
=1,
∴函数g(x)在x∈[-1,1]时,函数单调递减.
∴g(1)=2a+4,g(-1)=4-2a.
即4-2a≤g(x)≤4+2a,
若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,
即g(x)max≥f(x)max且g(x)min≤f(x)min,
则
,
即
,
此时a≥1,
∵a>0且a≠1,
∴a>1,
即a的取值范围是a>1;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,
即g(x)min≥f(x)max,
则4-2a≥a+
,
∴4-3a≥
,
∴3a2-4a+1≤0,
解得
≤a≤1,
∵a>0且a≠1,
∴
≤a<1,
即a的取值范围[
,1).
则f(-x)=ax+a-x=f(x),为偶函数,
设t=ax,则函数f(x)等价为y=t+
| 1 |
| t |
若a>1,当0≤x≤1时,t=ax单调递增,且t≥1,此时函数y=t+
| 1 |
| t |
若0<a<1,当0≤x≤1时,t=ax单调递减,且0<t≤1,此时函数y=t+
| 1 |
| t |
综上当x≥0时,函数单调递增,
∵函数f(x)是偶函数,∴当-1≤x≤0时,函数单调递减.
故函数的递增区间为[0,1],递减区间为[-1,0].
∴函数的值域为[2,a+
| 1 |
| a |
(2)∵a>0且a≠1,
∴g(x)=ax2-2ax+4-a(x∈[-1,1])的对称轴为x=-
| -2a |
| 2a |
∴函数g(x)在x∈[-1,1]时,函数单调递减.
∴g(1)=2a+4,g(-1)=4-2a.
即4-2a≤g(x)≤4+2a,
若对于任意x1∈[-1,1],总存在x0∈[-1,1],使得g(x0)=f(x1)成立,
即g(x)max≥f(x)max且g(x)min≤f(x)min,
则
|
即
|
此时a≥1,
∵a>0且a≠1,
∴a>1,
即a的取值范围是a>1;
(3)若对于任意x0∈[-1,1],任意x1∈[-1,1],都有g(x0)≥f(x1)恒成立,
即g(x)min≥f(x)max,
则4-2a≥a+
| 1 |
| a |
∴4-3a≥
| 1 |
| a |
∴3a2-4a+1≤0,
解得
| 1 |
| 3 |
∵a>0且a≠1,
∴
| 1 |
| 3 |
即a的取值范围[
| 1 |
| 3 |
点评:本题主要考查函数奇偶性和单调性的应用,利用复合函数单调性之间的关系是解决本题的关键,要注意区分存在性与恒成立型函数最值之间的关系.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
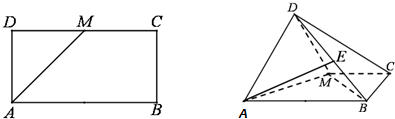
 在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E
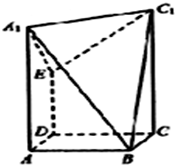
在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上且AG=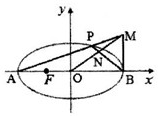 已知椭圆
已知椭圆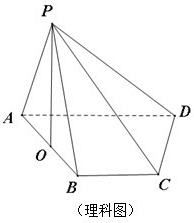 (理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.
(理科做)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠ABC=90°,BC∥AD,且AB=AD=2BC,顶点P在底面ABCD内的射影恰好落在AB的中点O上.