Question

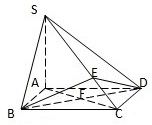已知四棱锥S-ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的任意一点．
（1）求证：平面EBD⊥平面SAC；
（2）当SA=AB时，求二面角B-SC-D的大小．

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面垂直的判定

专题：综合题,空间位置关系与距离,空间角

分析：（1）欲证平面EBD⊥平面SAC，只需证BD⊥面SAC，利用线面垂直的判定定理可证得；
（2）建立空间直角坐标系，求出平面BSC、平面SCD的法向量，利用向量的夹角公式，即可求二面角B-SC-D的大小．

解答： （1）证明：∵SA⊥底面ABCD，
∴SA⊥BD…（2分）
∵底面ABCD是正方形，
∴AC⊥BD…（4分）
∵SA∩AC=A，
∴BD⊥平面SAC，
又BD?平面EBD
∴平面EBD⊥平面SAC…（5分）
（2）解：如图所示建立空间直角坐标系，点A为坐标原点，AB，AD，AS所在的直线分别为x，y，z轴．设AB=1．

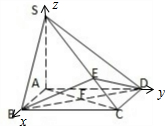
由题意得B（1，0，0），S（0，0，1），C（1，1，0），D（0，1，0）…（6分）

SB

=（1，0，-1），又

SC

=（1，1，-1）
设平面BSC的法向量为

n

（x₁，y₁，z₁），则

n • SC =x1+y1-z1=0 n • SB =x1-z1=0

，令z₁=1，则

n

=（1，0，1，…（8分）

DS

=（0，-1，1）

DC

=（1，0，0），
设平面SCD的法向量为

n

=（x₂，y₂，z₂），则

n2 • DC =x2=0 n • DS =z2-y2=0

，令y₂=1，则

n

=（0，1，1），…（10分）
设二面角B-SC-D的平面角为a，则
|cosα|=

| n1 • n2 |

| n1 |•| n2 |

=

1

2 × 2

=

1

2

．
显然二面角B-SC-D的平面角为α为钝角，所以α=120°，
即二面角C-PB-D的大小为20°．…（12分）

点评：本题主要考查了平面与平面之间的位置关系，考查向量法的运用，考查空间想象能力、运算能力和推理论证能力，属于中档题．