题目内容
设函数f（x）=ex+2x-4，g（x）=lnx+2x2-5，若实数a，b分别是f（x），g（x）的零点，则（ ）
| A、g（a）＜0＜f（b） |
| B、f（b）＜0＜g（a） |
| C、0＜g（a）＜f（b） |
| D、f（b）＜g（a）＜0 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：根据函数的解析式判断单调性，运用f（1）=e-2＞0，g（1）=0+2-5＜0，得出a＜1，b＞1，再运用单调性得出g（a）＜g（1）＜0，f（b）＞f（1）＞0，即可选择答案．
解答：
解：∵函数f（x）=ex+2x-4，g（x）=lnx+2x2-5，
∴f（x）与g（x）在各自的定义域上为增函数，
∵f（1）=e-2＞0，g（1）=0+2-5＜0，
∴若实数a，b分别是f（x），g（x）的零点，
∴a＜1，b＞1，
∵g（a）＜g（1）＜0，f（b）＞f（1）＞0，
故选：A
∴f（x）与g（x）在各自的定义域上为增函数，
∵f（1）=e-2＞0，g（1）=0+2-5＜0，
∴若实数a，b分别是f（x），g（x）的零点，
∴a＜1，b＞1，
∵g（a）＜g（1）＜0，f（b）＞f（1）＞0，
故选：A
点评：本题考查了函数的性质，运用单调性判断函数的零点的位置，再结合单调性求解即可．
练习册系列答案
相关题目
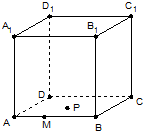如图，正方体ABCD-A1B1C1D1的棱长为1，点M在棱AB上，且PB，点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
下列说法正确的是（ ）
| A、“f（O）=O”是“函数f（x）是奇函数”的充要条件 | ||||||||
| B、“向量a，b，c，若a•b=a•c，则b=c”是真命题 | ||||||||
C、函数f（x）=
| ||||||||
D、“若α=
|
下列命题中的真命题是（ ）
A、?x∈R，sinx+
| ||
B、?x∈R，
| ||
| C、命题p：“?x∈R，x2-x-1＞0”的否定￢p：“?x∈R，x2-x-1≤0” | ||
| D、“ea＞eb”是“log2a＞log2b”的充要条件 |
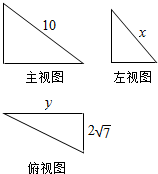
某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy的最大值为（ ）
| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|
阅读下面程序框图，则输出结果s的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
已知定义域为R的函数f（x）不是奇函数，给定下列4个命题：
①函数g（x）=f（-x）-f（x）是奇函数；
②?x∈R，f（-x）≠-f（x）；
③?x∈R，f（-x）=f（x）；
④?x0∈R，f（-x0）≠-f（x0）．
其中为真命题的命题是（ ）
①函数g（x）=f（-x）-f（x）是奇函数；
②?x∈R，f（-x）≠-f（x）；
③?x∈R，f（-x）=f（x）；
④?x0∈R，f（-x0）≠-f（x0）．
其中为真命题的命题是（ ）
| A、①② | B、②③ | C、③④ | D、①④ |
如图所示的程序框图中输出的结果为（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
正方体中两条面对角线的位置关系是（ ）
| A、平行 | B、异面 |
| C、相交 | D、平行、相交、异面都有可能 |