题目内容
求下列函数的导数
(1)g(x)=
(2)g(x)=x(x+1)(x-3)
(3)g(x)=excosx
(4)g(x)=x+2sinx
(5)h(x)=2x3-3x2+x-8
(6)u(x)=5-3x+2x2-x3.
(1)g(x)=
| x |
| 2+x2 |
(2)g(x)=x(x+1)(x-3)
(3)g(x)=excosx
(4)g(x)=x+2sinx
(5)h(x)=2x3-3x2+x-8
(6)u(x)=5-3x+2x2-x3.
考点:导数的运算
专题:导数的综合应用
分析:利用导数的运算法则即可得出.
解答:
解:(1)g′(x)=
=
;
(2)g(x)=x3-2x2-3x,∴g′(x)=3x2-4x-3;
(3)g′(x)=excosx-exsinx;
(4)g′(x)=1+2cosx;
(5)h′(x)=6x2-6x+1;
(6)u′(x)=-3+4x-3x2.
| 2+x2-x(2x) |
| (2+x2)2 |
| 2-x2 |
| (2+x2)2 |
(2)g(x)=x3-2x2-3x,∴g′(x)=3x2-4x-3;
(3)g′(x)=excosx-exsinx;
(4)g′(x)=1+2cosx;
(5)h′(x)=6x2-6x+1;
(6)u′(x)=-3+4x-3x2.
点评:本题考查了导数的运算法则,属于基础题.

练习册系列答案
相关题目
对数列{an},{bn},若区间[an,bn]满足下列条件:
①[an+1,bn+1]?[an,bn](n∈N*);
②
(bn-an)=0,
则称{[an,bn]}为区间套.下列选项中,可以构成区间套的数列是( )
①[an+1,bn+1]?[an,bn](n∈N*);
②
| lim |
| n→∞ |
则称{[an,bn]}为区间套.下列选项中,可以构成区间套的数列是( )
A、an=(
| ||||
B、an=(
| ||||
C、an=
| ||||
D、an=
|
在二项式(2x+1)6的展开式中,系数最大项的系数是( )
| A、20 | B、160 |
| C、240 | D、192 |
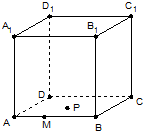 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
下列说法正确的是( )
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
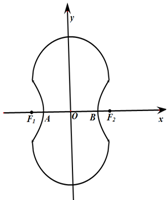 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶