题目内容
双曲线
-
=1与曲线
+
=1(a>0,b>0)的交点恰为某正方形的四个顶点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3a2 |
| y2 |
| b2 |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出两曲线的交点,由正方形的各边相等,得到a,b的关系,再由双曲线的a,b,c的关系,结合离心率公式,即可计算得到.
解答:
解:由双曲线
-
=1与曲线
+
=1(a>0,b>0),
解得,x2=
a2,y2=
b2.
即有交点为A(
a,
b),B(-
a,
b),
C(-
a,-
b),D(
a,-
b),
由于交点恰为某正方形的四个顶点,
则|AB|=|BC|,
即为
a=
b,即b=
a,
c=
=2a,
则有离心率为e=
=2.
故选B.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3a2 |
| y2 |
| b2 |
解得,x2=
| 3 |
| 2 |
| 1 |
| 2 |
即有交点为A(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
C(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
由于交点恰为某正方形的四个顶点,
则|AB|=|BC|,
即为
| 6 |
| 2 |
| 3 |
c=
| a2+b2 |
则有离心率为e=
| c |
| a |
故选B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,同时考查两曲线的交点问题,考查运算能力,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知平面α∥平面β,直线m?平面α,那么直线m与平面β 的关系是( )
| A、直线m在平面β内 |
| B、直线m与平面β相交但不垂直 |
| C、直线m与平面β垂直 |
| D、直线m与平面β平行 |
下列说法正确的是( )
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
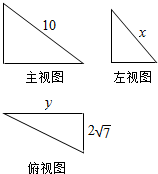
某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为( )

| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|
 如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧EB、EC(E在线段AD上).由两圆弧EB、EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为
如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧EB、EC(E在线段AD上).由两圆弧EB、EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为