题目内容
4.已知向量$\overrightarrow{OA}$=(1,-3),$\overrightarrow{OB}$=(2,-1),$\overrightarrow{OC}$=(k+1,k-2),若点A、B、C不能构成三角形,则实数k应满足的条件是( )| A. | k=-2 | B. | k=$\frac{1}{2}$ | C. | k=1 | D. | k=-1 |
分析 根据条件便知A,B,C三点共线,从而有$\overrightarrow{AC}=t\overrightarrow{AB}$,这样可求出$\overrightarrow{AC},\overrightarrow{AB}$的坐标带入上式便可建立关于t和k的二元一次方程组,解方程组即可得出k的取值.
解答 解:A、B、C三点不能构成三角形;
∴A、B、C三点共线;
∴存在实数t,使$\overrightarrow{AC}=t\overrightarrow{AB}$;
∴$\overrightarrow{OC}-\overrightarrow{OA}=t(\overrightarrow{OB}-\overrightarrow{OA})$;
∴(k+1,k-2)-(1,-3)=t[(2,-1)-(1,-3)];
(k,k+1)=(t,2t);
∴$\left\{\begin{array}{l}{k=t}\\{k+1=2t}\end{array}\right.$;
解得k=1.
故选:C.
点评 考查共线向量基本定理,向量减法的几何意义,以及向量坐标的减法和数乘运算.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
14.偶函数f(x)(x∈R)满足:f(4)=f(1)=0,且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式xf(x)<0的解集为( )
| A. | (-∞,-4)∪(4,+∞) | B. | (-∞,-4)∪(-1,0) | C. | (-4,-1)∪(1,4) | D. | (-∞,-4)∪(-1,0)∪(1,4) |
9.下列哪个不等式是一元二次不等式?( )
| A. | x2+$\sqrt{2}$x<-1 | B. | x2+$\sqrt{x}$+1<0 | C. | x2+$\frac{3}{x}$+1<0 | D. | x+1<0 |
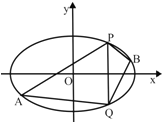 如图.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率e=$\frac{1}{2}$,椭圆C上一点M到左、右两个焦点F1、F2的距离之和是4.
如图.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率e=$\frac{1}{2}$,椭圆C上一点M到左、右两个焦点F1、F2的距离之和是4.