题目内容
19.已知平面向量$\overrightarrow{m}$=(2cosx,sinx),$\overrightarrow{n}$=(sinx,2sinx)(x∈R),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-1.(1)将函数f(x)的图象向右平移$\frac{π}{6}$个单位长度后得到g(x),求函数g(x)的最小正周期以及对称轴方程;
(2)当x∈[0,$\frac{π}{2}$]时,求函数f(x)的取值范围.
分析 (1)由向量的数量积和三角函数运算可得f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),由图象变换可得g(x)=$\sqrt{2}$sin(2x-$\frac{7π}{12}$),易得周期和对称轴;
(2)由x∈[0,$\frac{π}{2}$]结合三角函数的性质可得取值范围.
解答 解:(1)∵$\overrightarrow{m}$=(2cosx,sinx),$\overrightarrow{n}$=(sinx,2sinx),
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-1=2sinxcosx+2sin2x-1
=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∵将函数f(x)的图象向右平移$\frac{π}{6}$个单位长度后得到g(x),
∴g(x)=$\sqrt{2}$sin[2(x-$\frac{π}{6}$)-$\frac{π}{4}$]=$\sqrt{2}$sin(2x-$\frac{7π}{12}$),
∴函数g(x)的最小正周期T=$\frac{2π}{2}$=π,
由2x-$\frac{7π}{12}$=kπ+$\frac{π}{2}$可得x=$\frac{kπ}{2}$+$\frac{13π}{24}$,
∴对称轴方程为x=$\frac{kπ}{2}$+$\frac{13π}{24}$,k∈Z;
(2)当x∈[0,$\frac{π}{2}$]时,2x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],
∴sin(2x-$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],
∴$\sqrt{2}$sin(2x-$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
∴函数f(x)的取值范围为[-1,$\sqrt{2}$].
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和值域,属中档题.

 优百分课时互动系列答案
优百分课时互动系列答案| A. | f(x)=x2(x≥0) | B. | f(x)=-2x | C. | f(x)=3x-2 | D. | f(x)=x3 |
| A. | k=-2 | B. | k=$\frac{1}{2}$ | C. | k=1 | D. | k=-1 |
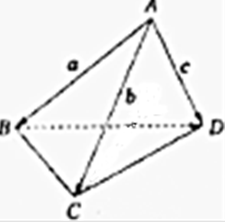 已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.
已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.