题目内容

14．设abc＞0，二次函数f（x）=ax2+bx+c的图象可能是下列图形中的①（填序号）．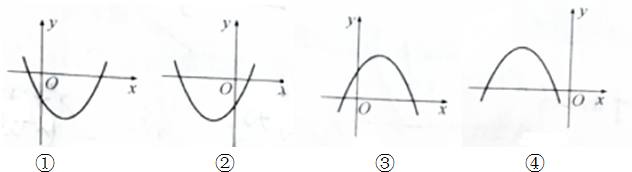

分析 当a＞0时，二次函数开口向上，判断①②中c的符号，再确定b的符号，判断①②的正误；当a＜0时，同样的方法判断③④的正误．

解答 解：当a＞0时，因为abc＞0，所以b、c同号，由①②两图中可知c＜0，
故b＜0，∴-$\frac{b}{2a}$＞0，即函数对称轴在y轴右侧，②不正确，①符合题意．
显然a＜0时，开口向下，因为abc＞0，所以b、c异号，
对于③，c＞0，对称轴-$\frac{b}{2a}$＜0，不正确．
对④，由图象可知c＜0，则b＞0，对称轴-$\frac{b}{2a}$＞0，不正确．
故答案为：①．

点评 根据二次函数图象开口向上或向下，分a＞0或a＜0两种情况分类考虑．另外还要注意c值是抛物线与y轴交点的纵坐标，还要注意对称轴的位置或定点坐标的位置等．是常考题．

练习册系列答案
相关题目
4．已知向量$\overrightarrow{OA}$=（1，-3），$\overrightarrow{OB}$=（2，-1），$\overrightarrow{OC}$=（k+1，k-2），若点A、B、C不能构成三角形，则实数k应满足的条件是（　　）
A．k=-2B．k=$\frac{1}{2}$C．k=1D．k=-1
5．如果复数$\frac{i}{2}$（1-ai）（其中i为虚数单位，a为实数）的实部和虚部互为相反数，那么a等于（　　）
A．1B．-1C．$\frac{1}{2}$D．-$\frac{1}{2}$
2．椭圆$\frac{{x}^{2}}{25}$$+\frac{{y}^{2}}{16}$=1上有一点M，其横坐标为2，则M到椭圆的右准线间的距离是（　　）
A．$\frac{19}{3}$B．$\frac{31}{3}$C．-$\frac{19}{3}$D．-$\frac{31}{3}$
9．求函数f（x）=4x+4-x-2x+2-x-4，x∈[0，1）的值域．
19．已知函数f（x）=ex，g（x）=x2+（1-t）x+1．
（1）若f（x）＞k（x+1）恒成立，求正实数k的取值范围．
（2）若存在x1，x2∈[0，1]，使得f（x1）g（x2）＞2f（x2）g（x1）成立，求实数t的取值范围．
6．函数f（x）=x2+$\frac{1}{{x}^{2}}$+1．
（1）求f（x）的定义域；
（2）判断f（x）的奇偶性；
（3）求f（x）的单调区间和最小值．
3．己知点H是xOy直角坐标平面上一动点，A（$\sqrt{5}$，0），B（0，2），C（0，-1）是平面上的定点．
（1）$\frac{|HB|}{|HA|}$=2时，求H的轨迹方程；
（2）当H在线段BC上移动，求$\frac{|HB|}{|HA|}$的最大值及H点坐标．
4．已知变量x，y满足约束条件$\left\{\begin{array}{l}{y≤2}\\{x+y≥1}\\{x-y≤1}\end{array}\right.$，则z=$\sqrt{{x}^{2}+{y}^{2}}$的最大值为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{5}$D．$\sqrt{13}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网