题目内容
2. 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | $\frac{41}{4}$π | D. | 12π |
分析 根据三视图得出空间几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,A,D为棱的中点,利用球的几何性质求解即可.
解答 解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,正方体的棱长为2,
A,D为棱的中点
根据几何体可以判断:球心应该在过A,D的平行于底面的中截面上,
设球心到截面BCO的距离为x,则到AD的距离为:2-x,
∴R2=x2+($\sqrt{2}$)2,R2=12+(2-x)2,
解得出:x=$\frac{3}{4}$,R=$\frac{\sqrt{41}}{4}$,
该多面体外接球的表面积为:4πR2=$\frac{41}{4}$π,
故选:C.
点评 本题综合考查了空间几何体的性质,学生的空间思维能力,构造思想,关键是镶嵌在常见的几何体中解决.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
12. 如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
 如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
13.已知a>b,c>d,且c,d不为零,那么( )
| A. | ad>bc | B. | ac>bd | C. | a-c>b-d | D. | a-d>b-c |
10.若复数z=$\frac{1+mi}{1+i}$(i是虚数单位)是实数,则实数m=( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
7.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是( )
| A. | 若m⊥α,m⊥β,则α⊥β | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若m∥α,m∥β,则α∥β | D. | 若m⊥α,n∥α,则m⊥n |
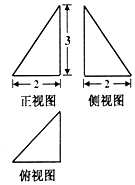 已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.
已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2. 如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.
如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.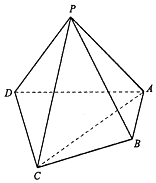 如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四凌锥中P-ABCD,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.