题目内容
12. 如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
分析 设AB=BC=2,取AB的中点为O,由题意可得双曲线的一条渐近线为直线OC,由余弦定理可得OC,cos∠COB,求得tan∠COB,即为渐近线的斜率,由a,b,c的关系和离心率公式,即可得到.
解答  解:设AB=BC=2,
解:设AB=BC=2,
取AB的中点为O,
由题意可得双曲线的一条渐近线为直线OC,
在三角形OBC中,
cosB=-$\frac{1}{2}$,
∴OC2=OB2+BC2-2OB•BC•cosB=1+4-2×1×2×(-$\frac{1}{2}$)=7,
∴OC=$\sqrt{7}$,
则cos∠COB=$\frac{7+1-4}{2\sqrt{7}}$=$\frac{2}{\sqrt{7}}$,
可得sin∠COB=$\sqrt{1-\frac{4}{7}}$=$\frac{\sqrt{3}}{\sqrt{7}}$,
tan∠COB=$\frac{sin∠COB}{cos∠COB}$=$\frac{\sqrt{3}}{2}$,
可得双曲线的渐近线的斜率为$\frac{\sqrt{3}}{2}$,
不妨设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
渐近线方程为y=±$\frac{b}{a}$x,
可得$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$,
可得e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{1+\frac{3}{4}}$=$\frac{\sqrt{7}}{2}$.
故选:D.
点评 本题考查双曲线的方程和性质,主要是渐近线和离心率,考查学生的计算能力,属于中档题.

| A. | (0,$\frac{1}{4a}$) | B. | ($\frac{a}{2}$,0) | C. | (0,$\frac{1}{2a}$) | D. | ($\frac{a}{4}$,0) |
| X | 1 | 2 | 3 | 4 |
| P | $\frac{49}{84}$ | a | $\frac{9}{84}$ | $\frac{1}{84}$ |
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | $\frac{41}{4}$π | D. | 12π |
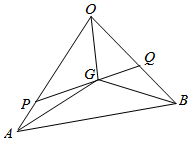 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.