题目内容
11. 如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.
如图,△ABC中,AC=2,BC=4,∠ACB=90°,D、E分别是AC、AB的中点,将△ADE沿DE折起成△PDE,使面PDE⊥面BCDE,H、F分别是边PD和BE的中点,平面BCH与PE、PF分别交于点I、G.(Ⅰ)求证:IH∥BC;
(Ⅱ)求二面角P-GI-C的余弦值.
分析 (Ⅰ)推导出DE∥BC,从而BC?平面BCH,由此能证明IH∥BC.
(Ⅱ)以D为原点,DE,DC,DP为x,y,z轴,建立空间右手直角坐标系,利用向量法能求出二面角P-GI-C的余弦值.
解答 证明:(Ⅰ)∵D,E分别是边AC和AB的中点,∴DE∥BC,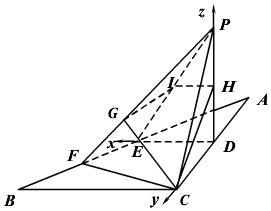
∵BC?平面PED,ED?平面PED,
∴BC?平面BCH,
∴IH∥BC.
解:(Ⅱ)如图,建立空间右手直角坐标系,由题意得:
D(0,0,0),E(2,0,0),P(0,0,1),F(3,$\frac{1}{2}$,0),C(0,1,0),H(0,0,$\frac{1}{2}$),
∴$\overrightarrow{EP}$=(-2,0,1),$\overrightarrow{EF}$=(1,$\frac{1}{2}$,0),$\overrightarrow{CH}$=(0,-1,$\frac{1}{2}$),$\overrightarrow{HI}$=$\frac{1}{2}\overrightarrow{DE}$=(1,0,0),
设平面PGI的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{EP}•\overrightarrow{n}=-2x+z=0}\\{\overrightarrow{EF}•\overrightarrow{n}=x+\frac{1}{2}y=0}\end{array}\right.$,令x=1,解得y=-2,z=2,∴$\overrightarrow{n}$=(1,-2,2),
设平面CHI的一个法向量为$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{CH}•\overrightarrow{m}=-b+\frac{1}{2}c=0}\\{\overrightarrow{HI}•\overrightarrow{m}=a=0}\end{array}\right.$,取b=1,得$\overrightarrow{m}$=(0,1,2),
设二面角P-GI-C的平面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{|-2+4|}{3×\sqrt{5}}$=$\frac{2\sqrt{15}}{15}$.
∴二面角P-GI-C的余弦值为$\frac{2\sqrt{15}}{15}$.
点评 本题考查线线平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| X | 1 | 2 | 3 | 4 |
| P | $\frac{49}{84}$ | a | $\frac{9}{84}$ | $\frac{1}{84}$ |
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | $\frac{41}{4}$π | D. | 12π |
| A. | |a|>|b| | B. | $\frac{b}{a}$<1 | C. | ab<b2 | D. | ab>b2 |

| A. | 10cm | B. | 8cm | C. | $(2\sqrt{3}+4)cm$ | D. | $4\sqrt{2}cm$ |