题目内容
用0,1,2,5,7,9组成没有重复数字的四位数,求出现下列各种情况的四位数的概率:
(1)2不在千位;
(2)能被25整除.
(1)2不在千位;
(2)能被25整除.
考点:排列、组合及简单计数问题
专题:概率与统计,排列组合
分析:先根据分类计数原理求出重复数字的四位数的个位,再分别求出2不在千位和能被25整除的四位数,根据概率公式计算即可.
解答:
解:0,1,2,5,7,9组成没有重复数字的四位数,需要分两类,第一类选0时,有
•
•
=180个,第二类,不选0时,有
=120个,根据分类计数原理的共有180+120=300个重复数字的四位数,
(1)2不在千位,当不选2也不选0时,有
=24个,当不选2选0时,有
•
•
=72个,当选2不选0时,有
•
•
=72个,当选2也选0时,有
•
=72个,故2不在千位的有24+3×72=240,
根据概率公式,2不在千位的四位数的概率为P=
=
;
(2),能倍25整除,后两位应该是25或50,当后两位为25时,
•
=9个,当后两位为50时,有
=13个,故被25整除的数有9+12=21,故能被25整除四位数的概率为
=
.
| A | 1 5 |
| C | 2 4 |
| A | 3 3 |
| A | 4 5 |
(1)2不在千位,当不选2也不选0时,有
| A | 4 4 |
| A | 1 4 |
| C | 2 3 |
| A | 3 3 |
| A | 1 4 |
| C | 2 3 |
| A | 3 3 |
| A | 1 4 |
| •C | 1 3 |
| A | 3 3 |
根据概率公式,2不在千位的四位数的概率为P=
| 240 |
| 300 |
| 4 |
| 5 |
(2),能倍25整除,后两位应该是25或50,当后两位为25时,
| A | 1 3 |
| A | 1 3 |
| A | 2 4 |
| 21 |
| 300 |
| 7 |
| 100 |
点评:本题主要考查了排列组合的问题和概率问题,关键是根据排列组合求出所满足条件的四位数,属于中档题.

练习册系列答案
相关题目
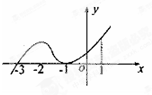 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:①-3是函数y=f(x)的极小值点;
②-1是函数y=f(x)的极值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
| A、①② | B、①④ | C、②③ | D、③④ |
设a=log0.34,b=log0.30.2,c=(
)π( )
| 1 |
| e |
| A、a>b>c |
| B、b>c>a |
| C、b>a>c |
| D、c>b>a |
已知函数f(x)是定义在(-6,6)上的偶函数,f(x)在[0,6]上是单调函数,且f(-2)≤f(1),f(-2)=25,那么下列肯定不正确的是( )
| A、f(1)≥25 |
| B、f(2)=25 |
| C、f(1)<25 |
| D、f(1)>25 |
 如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.
如图,两正方形ABCD、ABEF所成二面角大小为120°,求二面角D-AE-B的平面角的正切值.