题目内容
2.集合A={y|y=2x,x∈R},B={x∈Z|-2<x<4},则A∩B=( )| A. | {x|0<x<4} | B. | {1,2,3} | C. | {0,1,2,3} | D. | ∅ |
分析 根据指数函数的值域求出集合A,化简集合B,根据交集的定义写出A∩B.
解答 解:集合A={y|y=2x,x∈R}={y|y>0},
B={x∈Z|-2<x<4}={-1,0,1,2,3},
则A∩B={1,2,3}.
故选:B.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
14.若 x,y 满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y-4≤0\\ y≥0\end{array}\right.$,则 z=y-2x 的最大值为( )
| A. | 8 | B. | 4 | C. | 1 | D. | 2 |
17.已知命题p:函数y=lg(1-x)在(-∞,1)上单调递减,命题q:函数y=2cosx是偶函数,则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
7.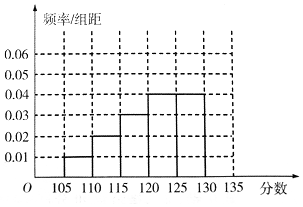 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取6份进行展出,并从6份试卷中选出两份作为优秀试卷,求优秀试卷分别来自两个分数段的概率.
 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110) | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取6份进行展出,并从6份试卷中选出两份作为优秀试卷,求优秀试卷分别来自两个分数段的概率.
11.“x>1”是“x2+2x>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |