题目内容
7. 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110) | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取6份进行展出,并从6份试卷中选出两份作为优秀试卷,求优秀试卷分别来自两个分数段的概率.
分析 (Ⅰ)根据频率=$\frac{样本容量}{总数}$,即可求出n,x,y的值,
(Ⅱ)先根据分层抽样求出第二组抽取的试卷份数为2份,第三组抽取的试卷份数为4份,并记第二组抽取的2份试卷为a,b,第三组抽取的4份试卷为A,B,C,D,一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
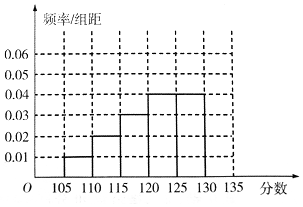
解答  解:(Ⅰ)图形如图所示:
解:(Ⅰ)图形如图所示:
由题意和频率分布直方图可得,第一组的频率为0.05,第一组的人数为$\frac{15}{0.3}$=50
∴$\frac{50}{n}$=0.05,
解的n=1000,
第三组的频率为0.03×5=0.15,则第三组的人数为1000×0.15=150
∴x=150×0.4=60
第6组的频率为1-(0.01+0.02+0.03+0.04+0.04)×5=0.30,
∴第六组的人数为1000×0.30=300,
∴y=$\frac{195}{300}$=0.65,
(Ⅱ)由[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取6份进行展出,
∵第二组和第三组的试卷份数为比为30:60=1:2,
∴第二组抽取的试卷份数为2份,第三组抽取的试卷份数为4份,
并记第二组抽取的2份试卷为a,b,第三组抽取的4份试卷为A,B,C,D,
则从6份试卷中选出两份作为优秀试卷,共有15种基本事件,分别为ab,aA,aB,aC,aD,bA,bB,bC,bD,AB,AC,AD,BC,BD,CD,
其中优秀试卷分别来自两个分数段有8种,分别为aA,aB,aC,aD,bA,bB,bC,bD,
故优秀试卷分别来自两个分数段的概率为$\frac{8}{15}$
点评 本题考查了频率分布直方图和古典概率的问题,属于基础题.

练习册系列答案
相关题目
15.复数z满足(z-i)(5-i)=26,则z的共轭复数为( )
| A. | -5-2i | B. | -5+2i | C. | 5-2i | D. | 5+2i |
2.集合A={y|y=2x,x∈R},B={x∈Z|-2<x<4},则A∩B=( )
| A. | {x|0<x<4} | B. | {1,2,3} | C. | {0,1,2,3} | D. | ∅ |
12.设U=R,A={-3,-2,-1,0,1,2},B={x|x≥1},则A∩∁UB=( )
| A. | {1,2} | B. | {-1,0,1,2} | C. | {-3,-2,-1,0} | D. | {2} |
17.已知函数$f(x)=a{x^3}-2{x^2}+\frac{1}{2}x+\frac{1}{3}$,若f(x)至少存在一个大于0的零点x0,则实数a的取值范围是( )
| A. | $(-∞,-\frac{10}{3}]$ | B. | $[-\frac{10}{3},+∞)$ | C. | $(-∞,\frac{7}{6}]$ | D. | $[\frac{7}{6},+∞)$ |