题目内容
14.在平面内将点A(2,1)绕原点按逆时针方向旋转$\frac{3π}{4}$,得到点B,则点B的坐标为(-$\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).分析 AC⊥x轴于C点,BD⊥x轴于D点,由点A的坐标得到AC,OC,可求sin∠AOC,cos∠AOC,再根据旋转的性质得到∠BOC=∠AOC+$\frac{3π}{4}$,OA=OB,利用两角和的正弦函数,余弦函数公式即可得到B点坐标.
解答 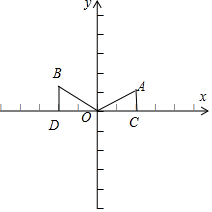 解:如图,作AC⊥x轴于C点,BD⊥x轴于D点,
解:如图,作AC⊥x轴于C点,BD⊥x轴于D点,
∵点A的坐标为(2,1),
∴AC=1,OC=2,
∴OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴sin∠AOC=$\frac{1}{\sqrt{5}}$,cos∠AOC=$\frac{2}{\sqrt{5}}$,
∵OA绕原点按逆时针方向旋转$\frac{3π}{4}$得OB,
∴∠AOB=$\frac{3π}{4}$,OA=OB=$\sqrt{5}$,
∴∠BOC=∠AOC+$\frac{3π}{4}$,
∴sin∠BOC=sin(∠AOC+$\frac{3π}{4}$)=sin∠AOCcos$\frac{3π}{4}$+cos∠AOCsin$\frac{3π}{4}$=$\frac{1}{\sqrt{5}}$×(-$\frac{\sqrt{2}}{2}$)+$\frac{2}{\sqrt{5}}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{10}}{10}$,
cos∠BOC=cos(∠AOC+$\frac{3π}{4}$)=cos∠AOCcos$\frac{3π}{4}$-sin∠AOCsin$\frac{3π}{4}$=$\frac{2}{\sqrt{5}}$×(-$\frac{\sqrt{2}}{2}$)-$\frac{1}{\sqrt{5}}$×$\frac{\sqrt{2}}{2}$=-$\frac{3\sqrt{10}}{10}$,
∴DB=OBsin∠BOC=$\sqrt{5}$×$\frac{\sqrt{10}}{10}$=$\frac{\sqrt{2}}{2}$,OD=OBcos∠BOC=$\sqrt{5}$×(-$\frac{3\sqrt{10}}{10}$)=-$\frac{3\sqrt{2}}{2}$,
∴B点坐标为:(-$\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
故答案为:(-$\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题考查了坐标与图形变化-旋转:把点旋转的问题转化为直角三角形旋转的问题,根据直角三角形的性质确定点的坐标.也考查了两角和与差的正弦函数公式的应用,考查了数形结合思想,属于中档题.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 已知输入的 x 值为1,执行如图所示的程序框图,则输出的结果为( )
已知输入的 x 值为1,执行如图所示的程序框图,则输出的结果为( )| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
| A. | {x|0<x<4} | B. | {1,2,3} | C. | {0,1,2,3} | D. | ∅ |
 根据此程序框图输出S的值为$\frac{11}{12}$,则判断框内应填入的是( )
根据此程序框图输出S的值为$\frac{11}{12}$,则判断框内应填入的是( )| A. | i≤8? | B. | i≤6? | C. | i≥8? | D. | i≥6? |
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |