题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,设S为△ABC的面积,且S=
(a2+b2-c2).
(1)求角C的大小;
(2)当cosA+cosB取得最大值时,判断△ABC的形状.
| ||
| 4 |
(1)求角C的大小;
(2)当cosA+cosB取得最大值时,判断△ABC的形状.
考点:三角形的形状判断,余弦定理
专题:解三角形
分析:(1)利用余弦定理得a2+b2-c2=2abcosC,将S=
(a2+b2-c2)与S=
absinC,联立即可求得tanC=
,而C∈(0,π),从而可得角C的大小;
(2)cosA+cosB=cosA+cos(
-A),利用两角差的余弦与两角和的正弦可求得当cosA+cosB取得最大值时,A的值,从而可判断△ABC的形状.
| ||
| 4 |
| 1 |
| 2 |
| 3 |
(2)cosA+cosB=cosA+cos(
| 2π |
| 3 |
解答:
解:(1)在△ABC中,由余弦定理可得a2+b2-c2=2abcosC,
∴S=
(a2+b2-c2)=
×2abcosC=
abcosC;
又S=
absinC,
∴tanC=
,C∈(0,π),
∴C=
;
(2)cosA+cosB=cosA+cos(
-A)=cosA+cos
cosA+sin
sinA=
cosA+
sinA=sin(A+
)≤1,
当A=
时,cosA+cosB取得最大值1,
此时△ABC为等边三角形.
∴S=
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
又S=
| 1 |
| 2 |
∴tanC=
| 3 |
∴C=
| π |
| 3 |
(2)cosA+cosB=cosA+cos(
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
当A=
| π |
| 3 |
此时△ABC为等边三角形.
点评:本题考查三角形形状的判断,着重考查余弦定理、正弦定理的综合应用,考查两角和与差的正弦、余弦,属于中档题.

练习册系列答案
相关题目
设函数f(x)(x∈R)满足f(x+2)=f(x)+2.当0≤x<2时,f(x)=1,则f(2014)=( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
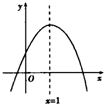 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是x=1.给出下列四个结论: