题目内容
已知x>y>2,且x+y,x-y,xy,
能依某种顺序构成等比数列,试求此等比数列.
| y |
| x |
考点:等比数列的性质
专题:等差数列与等比数列
分析:分①当
<x-y时和②当
>x-y 时两种情况,分别利用等比数列的定义和性质求得x、y的值,可得此等比数列.
| y |
| x |
| y |
| x |
解答:
解:由条件可得x-y<x+y<xy,故需讨论
和x-y的大小,
由于
<1,①当
<x-y时,
<x-y<x+y<xy,故由题意可得
、x-y、x+y、xy 依次构成等比数列,
∴
,求得x=1+5
,y=5+
,
∴此等比数列为:
、-4+
、6+
、10+
.
②当
>x-y,由x-y,
,x+y,xy顺次构成等比数列可得(x+y)2=
•(xy),求得x=-2y,这不满足条件x>y>2,
故这种情况不存在.
综上可得,此等比数列为:
、-4+
、6+
、10+
.
| y |
| x |
由于
| y |
| x |
| y |
| x |
| y |
| x |
| y |
| x |
∴
|
| 2 |
| ||
| 2 |
∴此等比数列为:
| ||
| 2 |
9
| ||
| 2 |
11
| ||
| 2 |
51
| ||
| 2 |
②当
| y |
| x |
| y |
| x |
| y |
| x |
故这种情况不存在.
综上可得,此等比数列为:
| ||
| 2 |
9
| ||
| 2 |
11
| ||
| 2 |
51
| ||
| 2 |
点评:本题主要考查等比数列的定义和性质,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
已知全集U=R,集合A={x|a≤x≤b},集合B={x|x2-x-2>0},若A∩B=φ,A∪B=U,则a,b的值分别是( )
| A、-1,2 | B、2,-1 |
| C、-1,1 | D、-2,2 |
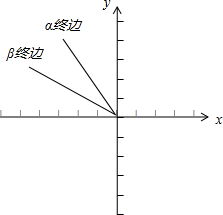 已知α是第二象限角,在第二象限内将角α的终边绕原点按逆时针方向旋转,得到第二象限角β的终边,如图所示,利用单位圆中的三角函数线比较下列各组数的大小.
已知α是第二象限角,在第二象限内将角α的终边绕原点按逆时针方向旋转,得到第二象限角β的终边,如图所示,利用单位圆中的三角函数线比较下列各组数的大小.