题目内容
9.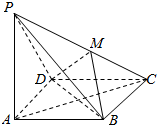 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.(1)求证:BD⊥平面PAC.
(2)求证:平面MBD⊥平面PCD.
分析 (1)证明BD垂直于平面PAC中两条相交直线,即可证明BD⊥平面PAC.
(2)证明PC⊥平面DBM,即可证明平面MBD⊥平面PCD.
解答  证明:(1)连结AC,
证明:(1)连结AC,
∵底面ABCD是正方形,
∴BD⊥AC,
∵PA⊥底面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵PA∩AC=A,∴BD⊥平面PAC.
(2)由(1)知BD⊥平面PAC,
∵PC?平面PAC,
∴BD⊥PC,
∵DM⊥PC,BD∩DM=D,
∴PC⊥平面DBM,
∵PC?平面PDC,
∴平面MBD⊥平面PCD.
点评 本题考查平面与平面垂直的判定,考查线面垂直,考查学生分析解决问题的能力,正确证明线面垂直是关键.

练习册系列答案
相关题目
2.在正方体ABCD-A1B1C1D1中,E是AB的中点,且正方体棱长为2,则异面直线DE与B1C的夹角的余弦值为( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | -$\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | -$\frac{\sqrt{10}}{5}$ |
4.已知三棱锥P-ABC,在底面△ABC中,∠A=60°,$BC=\sqrt{3}$,PA⊥面ABC,PA=2,则此三棱锥的外接球的体积为( )
| A. | $\frac{{8\sqrt{2}}}{3}π$ | B. | $4\sqrt{3}π$ | C. | $\frac{{4\sqrt{2}π}}{3}$ | D. | 8π |
18.为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:
男生:
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
(${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
女生:
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 2 | 4 | 8 | 4 | 2 |
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 1 | 5 | 6 | 5 | 3 |
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
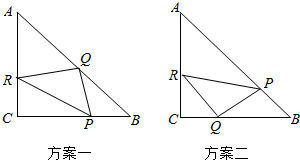 在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:
在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案: