题目内容
17．若函数y=loga（x+b）（a＞0，a≠1）的图象过两点（-1，0）和（0，$\frac{1}{2}$），则实数a=4，b=2．分析 由已知可得$\left\{\begin{array}{l}{0=lo{g}_{a}（-1+b）}\\{\frac{1}{2}=lo{g}_{a}（0+b）}\end{array}\right.$，解得a，b．
解答 解：∵函数y=loga（x+b）（a＞0，a≠1）的图象过两点（-1，0）和（0，$\frac{1}{2}$），
∴$\left\{\begin{array}{l}{0=lo{g}_{a}（-1+b）}\\{\frac{1}{2}=lo{g}_{a}（0+b）}\end{array}\right.$，解得a=4，b=2．
故答案分别为：4；2．
点评 本题考查了对数与指数函数的运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
10．垂直于两条异面直线的直线有（ ）条．
| A． | 1 | B． | 2 | C． | 无数 | D． | 以上都不对 |
8．设{an}是任意的等比数列，它的前n项和，前2n项和与前3n项和分别为P，Q，R，则下列等式中恒成立的为（ ）
| A． | P+R=2Q | B． | Q（Q-P）=P（R-P） | C． | Q（Q-P）=R | D． | Q2=PR |
5．若函数f（x）=$\left\{\begin{array}{l}（3a-1）x+4a，\;（x＜1）\\ \frac{a}{x}，\;x≥1\end{array}$是（-∞，+∞）上的减函数，则a的取值范围是（ ）
| A． | $a＜\frac{1}{3}$ | B． | $a≤\frac{1}{3}$ | C． | $\frac{1}{6}≤a＜\frac{1}{3}$ | D． | $0＜a＜\frac{1}{3}$ |
12．设复数w=（$\frac{a+i}{1+i}$）2，其中a为实数，若w的实部为2，则w的虚部为（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{2}$ |
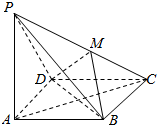如图，在四棱锥P-ABCD中，PA⊥底面ABCD，且底面ABCD是正方形，DM⊥PC，垂足为M．
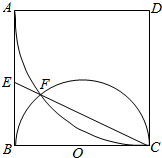如图，四边形为边长为a的正方形，以D为圆心，DA为半径的圆弧与以BC为直径的圆O交于C，F，连接CF并延长交AB于点E．