题目内容
正方形ABCD沿对角线AC折成直二面角，则异面直线AD和BC所成角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：异面直线及其所成的角
专题：空间角
分析：以AC的中点O为坐标原点，OA为x轴正半轴，OB为y轴正半轴，OD为z轴正半轴建立空间直角坐标系O-xyz，标出各点坐标，从而得向量
和
的坐标，由公式cos＜
，
＞=
，可探求异面直线AD和BC所成角．
| AD |
| BC |
| AD |
| BC |
| ||||
|
|
解答：
解：在原正方形中，设AC与BD的交点为O，沿AC折成直二面角后，由OD⊥AC及OB⊥AC知，∠BOD=90°，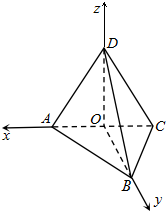
于是以O为坐标原点，OA为x轴正半轴，OB为y轴正半轴，OD为z轴正半轴建立空间直角坐标系O-xyz，如右图所示．
又设原正方形的边长为2，则A（-
，0，0），B（0，
，0），C（
，0，0），D（0，0，
），
从而
=（
，0，
），
=（
，-
，0），得|
|=2，|
|=2，
所以cos＜
，
＞=
=
=
，
又异面直线AD和BC所成角的范围是（0，
]，得异面直线AD和BC所成的角为
．
故答案为B．
于是以O为坐标原点，OA为x轴正半轴，OB为y轴正半轴，OD为z轴正半轴建立空间直角坐标系O-xyz，如右图所示．
又设原正方形的边长为2，则A（-
| 2 |
| 2 |
| 2 |
| 2 |
从而
| AD |
| 2 |
| 2 |
| BC |
| 2 |
| 2 |
| AD |
| BC |
所以cos＜
| AD |
| BC |
| ||||
|
|
| ||||||||
| 2×2 |
| 1 |
| 2 |
又异面直线AD和BC所成角的范围是（0，
| π |
| 2 |
| π |
| 3 |
故答案为B．
点评：本题主要考查了两异面直线所成角的求法，当几何体中出现面面垂直关系时，可以考虑使用向量法求解，应注意区分两向量的夹角与两异面直线所成角的关系，一般来说，若两向量夹角为钝角，则两异面直线所成角是其补角；若两向量夹角为锐角，则两异面直线所成角就是该角．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
化简4x
(-3x
y-
)÷(-6x-
y-
)=（ ）
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、2xy
| ||
B、-2xy
| ||
| C、2y | ||
| D、-2y-1 |
若函数y=sin2x+m•cosx+
m-
在闭区间[0，
]上的最大值是1，则满足条件的m值为（ ）
| 5 |
| 8 |
| 3 |
| 2 |
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，四面体A-BCD中，AD⊥面BCD，BC⊥CD，AD=2，BD=2