题目内容
已知定义在R上的奇函数f（x）的导函数为f′（x），当x＜0时，f（x）满足2f（x）+xf′（x）＜xf（x），则f（x）在R上的零点个数为（ ）
| A、1 | B、3 | C、5 | D、1或3 |
考点：导数的运算,根的存在性及根的个数判断
专题：函数的性质及应用
分析：可构造函数F（x）=
（x＜0），对其求导，利用导数判断其单调性，结合函数为奇函数，即可得出结论．
| x2f(x) |
| ex |
解答：
解：构造函数F（x）=
（x＜0），
所以F′（x）=
=
，
因为2f（x）+xf′（x）＜xf（x），x＜0，
所以F′（x）＞0，
所以函数F（x）在x＜0时是增函数，
又F（0）=0 所以当x＜0，F（x）＜F（0）=0成立，
因为对任意x＜0，
＞0，所以f（x）＜0，
由于f（x）是奇函数，所以x＞0时f（x）＞0，
即f（x）=0只有一个根就是0．
故选A．
| x2f(x) |
| ex |
所以F′（x）=
| 2xf(x)ex+x2f′(x)ex-x2f(x)ex |
| (ex)2 |
| x[2f(x)+xf′(x)-xf(x)] |
| ex |
因为2f（x）+xf′（x）＜xf（x），x＜0，
所以F′（x）＞0，
所以函数F（x）在x＜0时是增函数，
又F（0）=0 所以当x＜0，F（x）＜F（0）=0成立，
因为对任意x＜0，
| x2 |
| ex |
由于f（x）是奇函数，所以x＞0时f（x）＞0，
即f（x）=0只有一个根就是0．
故选A．
点评：本题考查了函数零点的判断；本题的难点在于构造新函数F（x）=
，通过求导判断函数的单调性．
| x2f(x) |
| ex |
练习册系列答案
相关题目
已知a=（
）
，b=log2
，c=log
，则（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、c＞b＞a |
函数f（x）=
的定义域为（ ）
log
|
| A、（3，+∞） |
| B、[3，+∞） |
| C、（3，4] |
| D、（-∞，4] |
正方形ABCD沿对角线AC折成直二面角，则异面直线AD和BC所成角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
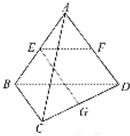如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：