题目内容
9. 每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:
每年七夕,琳琅满目的饰品在各大品牌店中成为年轻人亲眯的对象,这也使各大珠宝公司挖空心思,设计出匠心独运的饰品.某珠宝公司市场专员甲对该公司的一款项链的单价x(百元)和单位时间内的销售量y(件)之间的关系作出价格分析,所得数据如下:| 单价x(百元) | a1 | a2 | a3 | a4 | a5 |
| 单位时间内销售量y(件) | 14 | 13 | 10 | 7 | 5 |
(1)请根据上述数据在下列网格纸中绘制散点图;
(2)请根据表格数据计算项链的单价x(百元)和单位时间内的销售量y(件)之间的回归直线方程.
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
分析 (1)根据等差数列{an}的前10项和为230求出{an}的通项公式,写出前5项,作出散点图.
(2)计算$\overline{x},\overline{y}$,根据公式计算回归系数,得出回归方程.
解答 解:(1)∵{an}公差d=2,则a10=a1+9d=a1+18,∴S10=$\frac{{a}_{1}+{a}_{10}}{2}×10$=230,解得a1=14.∴a2=16,a3=18,a4=20,a5=22.
作出散点图如下: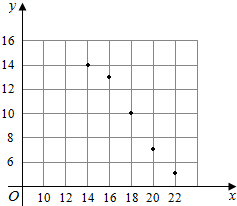
(2)$\overline{x}$=a3=18,$\overline{y}$=$\frac{1}{5}$(14+13+10+7+5)=9.5.
$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=14×14+16×13+18×10+20×7+22×5=834,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=142+162+182+202+222=1660.
∴$\stackrel{∧}{b}$=$\frac{834-5×18×9.5}{1660-5×1{8}^{2}}$=-0.53,$\stackrel{∧}{a}$=9.5+0.53×18=19.04.
∴项链的单价x(百元)和单位时间内的销售量y(件)之间的回归直线方程为y=-0.53x+19.04.
点评 本题考查了等差数列,散点图,回归方程计算,属于基础题.

练习册系列答案
相关题目
20.已知点(x,y)满足(x-1)2+(y-1)2≤1,则满足(y-x)(y-$\frac{1}{x}$)≥0的概率为( )
| A. | $\frac{π}{2}$ | B. | $\frac{4}{7}$π | C. | $\frac{1}{2}$ | D. | $\frac{4}{7}$ |
17.已知函数f(x)=|2x-1|,g(x)=x2-(2+3k)x+2k+1,若函数y=g[f(x)]有3个不同零点,则k的范围是( )
| A. | k=-$\frac{1}{2}$或k>0 | B. | -$\frac{1}{2}$<k<0或k>0 | C. | k≥-$\frac{1}{2}$ | D. | k≥0 |
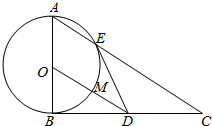 如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,在△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.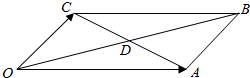 在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).
在下图平行四边形?OABC中,两对角线OB与AC相交于点D,若$\overrightarrow{OA}$=(3,1),$\overrightarrow{OC}$=(1,3),则向量$\overrightarrow{OD}$的坐标是(2,2).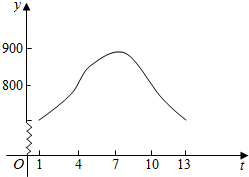 某地昆虫种群数量在七月份1~13日的变化如图所示,且满足y=Asin(ωx+φ)(ω>0,φ<0).
某地昆虫种群数量在七月份1~13日的变化如图所示,且满足y=Asin(ωx+φ)(ω>0,φ<0).