题目内容
8.设a=sin1,b=cos1,c=tan1,则( )| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
分析 在单位圆中,做出锐角1的正切线、正弦线、余弦线,观察他们的长度,可得sin1、cos1、tan1的大小关系.
解答  解:如图:在单位圆中,做出锐角1的正切线$\overrightarrow{AT}$、正弦线$\overrightarrow{MP}$、余弦线$\overrightarrow{OM}$,观察他们的长度,
解:如图:在单位圆中,做出锐角1的正切线$\overrightarrow{AT}$、正弦线$\overrightarrow{MP}$、余弦线$\overrightarrow{OM}$,观察他们的长度,
发现正切线最长,余弦线最短,
故有 tan1>sin1>cos1>0,即 b<a<c,
故选C.
点评 本题考查利用单位圆中的正切线、正弦线、余弦线的大小来比较对应的三角函数的大小,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
17.设Sn是等差数列{an}的前n项和,若$\frac{a_7}{a_4}=\frac{7}{13}$,则$\frac{{{S_{13}}}}{S_7}$=( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
15.已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为( )
| A. | $\frac{1-a}{2}$ | B. | $\frac{a}{2}$ | C. | 1-a | D. | $\frac{1+a}{2}$ |
3.国家标准规定:轻型汽车的氮氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆,对其氮氧化物的排放量进行检测,检测结果记录如下(单位:mg/km)
(Ⅰ)从被检测的5辆A型号的出租车和5辆B型号的出租车中分别抽取2辆,求抽取的这4辆车的氮氧化物排放量均不超过80mg/km的概率;
(Ⅱ)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为ξ,求ξ的分布列.
| A | 85 | 80 | 85 | 60 | 90 |
| B | 70 | 90 | 95 | 70 | 75 |
(Ⅱ)从被检测的5辆B种型号的出租车中任取2辆,记“氮氧化物排放量超过80mg/km”的车辆数为ξ,求ξ的分布列.
13.已知F1(-3,0),F2(3,0),满足条件|PF1|-|PF2|=2m-1的动点P的轨迹是双曲线的一支.下列数据:①2;②-1;③4;④-3;⑤$\frac{1}{2}$,则m可以是( )
| A. | ①③ | B. | ①② | C. | ①②⑤ | D. | ②④ |
20.函数g(x)=2x+5x的零点所在的一个区间是 ( )
| A. | (0,1) | B. | (1,2) | C. | (-1,0) | D. | (-2,-1) |
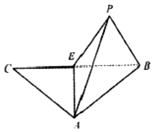 等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.
等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.