题目内容
如图所示,四棱锥P-ABCD中,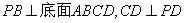 底面ABCD为直角梯形,
底面ABCD为直角梯形,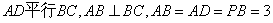 ,点E在棱PA上,且PE=2EA.
,点E在棱PA上,且PE=2EA.
(1) 求异面直线PA与CD所成的角;
(2) 求证:PC平行平面EBD;
(3) 求二面角A-BE-D的平面角的余弦值。
解:(Ⅰ)
在直角梯形ABCD中,AB=AD=3,
取BC的中点F,连接PF,AF,则AF//CD
 …………………2分
…………………2分

即 为
为 4分
4分
(Ⅱ)连接AC交BD于G,连EG,
又
又 …………………………………8
…………………………………8
(III)
又
作
在 。
。
在
 12
12

练习册系列答案
相关题目
 两侧,则a的取值范围是( )
两侧,则a的取值范围是( ) B.
B. C.
C. D.
D.
 与椭圆
与椭圆 交于
交于 两点,设线段
两点,设线段 的中点为P.若直线
的中点为P.若直线 (
( 0),直线OP的斜率为
0),直线OP的斜率为 ,则
,则 D.
D.
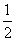 B最小值
B最小值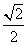 D最小值
D最小值 ,那么2x-y的最大值为_______.
,那么2x-y的最大值为_______. 的虚部为____________.
的虚部为____________. 满足
满足 ,且
,且 ,
, . 则有穷数列{
. 则有穷数列{ }(
}(  )的前
)的前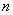 项和大于
项和大于 的概率是____________ .
的概率是____________ . 