题目内容
将函数y=cos(2x-
π)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:直接由函数图象的平移得到平移后的函数解析式,再由所得图象关于y轴对称,知平移后的函数为偶函数,结合三角函数的诱导公式可得2φ-
π=kπ,k∈Z.再结合φ的范围求得φ的最小值.
| 4 |
| 3 |
解答:
解:把函数y=cos(2x-
π)的图象向左平移φ(φ>0)个单位,
得到的函数解析式为y=cos[2(x+φ)-
π]=cos(2x+2φ-
π),
∵所得图象关于y轴对称,
∴y=cos(2x+2φ-
π)为偶函数,
则2φ-
π=kπ,k∈Z.
即φ=
+
π,k∈Z.
∵φ>0,
∴k=-1时,φ有最小值为
.
故选:A.
| 4 |
| 3 |
得到的函数解析式为y=cos[2(x+φ)-
| 4 |
| 3 |
| 4 |
| 3 |
∵所得图象关于y轴对称,
∴y=cos(2x+2φ-
| 4 |
| 3 |
则2φ-
| 4 |
| 3 |
即φ=
| kπ |
| 2 |
| 2 |
| 3 |
∵φ>0,
∴k=-1时,φ有最小值为
| π |
| 6 |
故选:A.
点评:本题主要考查三角函数的平移,三角函数的平移原则为左加右减上加下减.考查函数奇偶性的性质,属中档题.

练习册系列答案
相关题目
已知f(x)=cos(ωx+
)的图象与y=1的图象的两相邻交点间的距离为π,要得到y=f(x)的图象,只需把y=sinωx的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
不等式组
的解集为( )
|
| A、(-∞,-2]∪[3,4) |
| B、(-∞,-2]∪(4,+∞) |
| C、(4,+∞) |
| D、(-∞,-2]∪(4,+∞) |
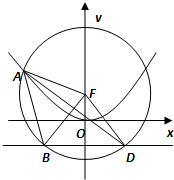 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4