题目内容
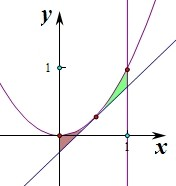
过抛物线y=x2上一动点P(t,t2) (0<t<1)作此抛物线的切线l,抛物线y=x2与直线x=0、x=1及切线l围成的图形的面积为S,则S的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:求出函数的导数,利用导数的几何意义求出切线方程,然后根据积分的几何意义求积分,利用积分函数即可S的最小值.
解答:
 解:∵y=f(x)=x2,
解:∵y=f(x)=x2,
∴f'(x)=2x,
即切线l在P处的斜率k=f'(t)=2t,
∴切线方程为y-t2=2t(x-t)=2tx-2t2,
即y-t2=2t(x-t)=2tx-2t2,
y=2tx-t2,
作出对应的图象,
则曲线围成的面积S=
(x2-2tx+t2)dx=(
x3-tx2+t2x)
=t2-t+
=(t-
)2+
,
∵0<t<1,
∴当t=
时,面积取的最小值为
.
故选:A.
 解:∵y=f(x)=x2,
解:∵y=f(x)=x2,∴f'(x)=2x,
即切线l在P处的斜率k=f'(t)=2t,
∴切线方程为y-t2=2t(x-t)=2tx-2t2,
即y-t2=2t(x-t)=2tx-2t2,
y=2tx-t2,
作出对应的图象,
则曲线围成的面积S=
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
∵0<t<1,
∴当t=
| 1 |
| 2 |
| 1 |
| 12 |
故选:A.
点评:本题主要考查积分的应用,利用导数的几何意义求出切线方程,然后根据积分公式即可得到面积的最小值,考查学生的计算能力.

练习册系列答案
相关题目
在△ABC中a、b、c分别是角A、B、C的对边,
=
,角A=( )
| tanA |
| tanB |
| ||
| b |
| A、30° | B、45° |
| C、60° | D、90° |
已知函数f(x)=(cosx-m)2+1在cosx=-1时取得最大值,在cosx=m时取得最小值,则实数m的取值范围是( )
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
已知扇形AOB的周长为8cm,面积为3cm2,则其圆心角为( )
A、6或
| ||||
B、6或
| ||||
C、
| ||||
D、
|
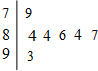 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )| A、85,84 |
| B、84,85 |
| C、86,84 |
| D、84,86 |
函数y=cos2(x+
)-cos2(x-
)是( )
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的偶函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为π的奇函数 |
将函数y=cos(2x-
π)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.
在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.