题目内容
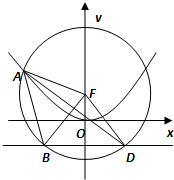 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4| 2 |
考点:圆与圆锥曲线的综合
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:求出圆F的半径|FA|=
p,A到l的距离,利用△ABD的面积为4
,求出p的值,即可得到圆F的方程.
| 2 |
| 2 |
解答:
解:由已知可得△BFD为等腰直角三角形,|BD|=2p,
圆F的半径|FA|=
p.…(3分)
由抛物线定义可知A到l的距离d=|FA|=
p.…(6分)
因为△ABD的面积为4
,所以
|BD|•d=4
,即
•2p•
p=4
,
解得p=-2(舍去),p=2.…(10分)
所以F(0,1),圆F的方程为x2+(y-1)2=8.…(12分)
圆F的半径|FA|=
| 2 |
由抛物线定义可知A到l的距离d=|FA|=
| 2 |
因为△ABD的面积为4
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解得p=-2(舍去),p=2.…(10分)
所以F(0,1),圆F的方程为x2+(y-1)2=8.…(12分)
点评:本题考查圆的方程,考查抛物线的定义,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
把函数y=sin2x的图象向左平移
个单位长度,再把所得图象所有点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的解析式为( )
| π |
| 4 |
| A、y=sinx | ||
| B、y=cosx | ||
C、y=sin(x+
| ||
| D、y=-sinx |
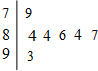 如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )| A、85,84 |
| B、84,85 |
| C、86,84 |
| D、84,86 |
对一个样本容量为100的数据分组,各组的频数如表:
估计小于29的数据大约占总体的( )
| 区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
| 频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
| A、42% | B、58% |
| C、40% | D、16% |
将函数y=cos(2x-
π)的图象向左平移φ(φ>0)个单位,所得图象关于y轴对称,则φ的最小值为( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|