题目内容
3.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线方程为2x+y=0,则C的离心率为( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 由题意设出双曲线的方程,得到它的一条渐近线方程y=$\frac{b}{a}$x即y=-2x,由此可得b:a=2:1,结合双曲线的平方关系可得c与a的比值,求出该双曲线的离心率.
解答 解:∵双曲线的方程为 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$,
∴双曲线的渐近线方程为y=±$\frac{b}{a}$x,结合题意一条渐近线方程为y=-2x,
得 b:a=2:1,
设a=t,b=2t,则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$t(t>0)
∴该双曲线的离心率是e=$\frac{c}{a}$=$\frac{\sqrt{5}t}{t}$=$\sqrt{5}$,
故选:D.
点评 本题考查双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
13.定义运算$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,复数z满足$|\begin{array}{l}{z}&{1}\\{i}&{i}\end{array}|$=2+i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.已知i为虚数单位,复数z满足z(1-i)=3+2i,则z=( )
| A. | $\frac{1}{2}$+$\frac{5i}{2}$ | B. | -$\frac{1}{2}$-$\frac{5i}{2}$ | C. | $\frac{5}{2}$+$\frac{5i}{2}$ | D. | -$\frac{5}{2}$-$\frac{5i}{2}$ |
11.已知复数z=$\frac{a+i}{2i}$(其中i为虚数单位)的虚部与实部相等,则实数a的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -1 | D. | $-\frac{1}{2}$ |
6.将圆C:(x-1)2+y2=25按向量$\overrightarrow{a}$=(1,1)平移得到圆C′,则圆C′的圆心和半径分别为( )
| A. | (1,0),5 | B. | (0,1),5 | C. | (-1,0),5 | D. | (2,1),5 |
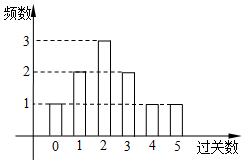 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.