题目内容
17.一个几何体的三视图如图所示,则该几何体的体积是( )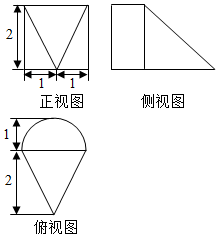
| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |
分析 几何体为半圆柱与四棱锥的组合体.
解答 解:由三视图可知几何体为半圆柱与四棱锥的组合体,半圆柱的底面半径为1,高为2,
四棱锥的底面是边长为2的正方形,棱锥的高为2.
所以几何体的体积V=$\frac{1}{2}π×{1}^{2}×2$+$\frac{1}{3}×{2}^{2}×2$=$π+\frac{8}{3}$.
故选:A.
点评 本题考查了空间几何体的三视图和体积计算,属于基础题.

练习册系列答案
相关题目
12.在△ABC中,p:△ABC是等边三角形,q:a:b:c=sinB:sinC:sinA,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.某单位共有10名员工,他们某年的收入如表:
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于5万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正线性相关关系,若某员工工作第一年至第四年的年薪分别为3万元、4.2万元、5.6万元、7.2万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\hat y=\hat bx+\hat a$中系数计算公式:$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{{{(\;{x_i}-\overline x\;)}^2}}}$,$\hat a=\overline y-\hat b\;\overline x$,其中$\overline x$、$\overline y$表示样本均值.
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(2)从该单位中任取2人,此2人中年薪收入高于5万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正线性相关关系,若某员工工作第一年至第四年的年薪分别为3万元、4.2万元、5.6万元、7.2万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\hat y=\hat bx+\hat a$中系数计算公式:$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{{{(\;{x_i}-\overline x\;)}^2}}}$,$\hat a=\overline y-\hat b\;\overline x$,其中$\overline x$、$\overline y$表示样本均值.
6.在空间中,设m,n为两条不同直线,α,β为两个不同平面,则下列命题正确的是( )
| A. | 若m∥α且α∥β,则m∥β | |
| B. | 若α⊥β,m?α,n?β,则m⊥n | |
| C. | 若m⊥α且α∥β,则m⊥β | |
| D. | 若m不垂直于α,且n?α,则m必不垂直于n |
7.下列命题正确的是( )
| A. | 空间四面体的四个顶点到平面α的距离相等.则α个数最多有4个 | |
| B. | 如果平面α与平面β同时垂直于平面γ,则α∥β | |
| C. | 如果三棱锥的三条侧棱两两垂直,则顶点在底面的射影一定是底面三角形的垂心 | |
| D. | 过空间中的任意一点P都可以作出同时与异面直线a,b平行的平面 |
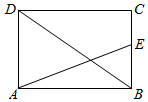
 如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.
如图,在几何体ABCDEF中,等腰梯形ABCD所在的平面与正方形CDEF所在的平面互相垂直,已知AB∥CD,AB=2BC=4,∠ABC=60°,点M是线段AC的中点.