题目内容
12.在△ABC中,p:△ABC是等边三角形,q:a:b:c=sinB:sinC:sinA,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 p:△ABC是等边三角形,可得:q:a:b:c=sinB:sinC:sinA.反之可得:a:b:c=b:c:a,即$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$,a2=bc,b2=ac,c2=ab,
再利用余弦定理、基本不等式的性质、三角形求值即可得出.
解答 解:p:△ABC是等边三角形,可得:q:a:b:c=sinB:sinC:sinA.
反之可得:a:b:c=b:c:a.∴$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$.
∴a2=bc,b2=ac,c2=ab,
利用余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$≥$\frac{2bc-bc}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),∴$A≤\frac{π}{3}$,同理可得:$B≤\frac{π}{3}$,C$≤\frac{π}{3}$,
∴A=B=C=$\frac{π}{3}$.
∴p是q的充要条件.
故选:C.
点评 本题考查了充要条件的判定方法、余弦定理、基本不等式的性质、三角形求值,考查了推理能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
3.下列各组中成等比数列的是( )
| A. | $\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$ | B. | 2,-2$\sqrt{2}$,4 | C. | 4,8,12 | D. | lg2,lg4,lg8 |
17.设函数y=log2$\frac{3}{x-1}$的定义域为集合A,函数y=$\root{3}{x-2}$的定义域为集合B,则A∩B为( )
| A. | {x|x≥2} | B. | {x|x≠1} | C. | {x|x>2} | D. | {x|x>1} |
16.已知集合B={1},A∪B={1,2},则A=( )
| A. | ∅ | B. | {2} | C. | {1,2} | D. | {2}或{1,2} |
17.一个几何体的三视图如图所示,则该几何体的体积是( )
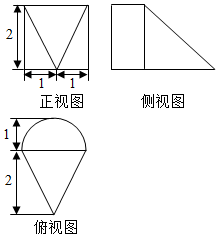

| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |