题目内容
5.某单位共有10名员工,他们某年的收入如表:| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪(万元) | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
(2)从该单位中任取2人,此2人中年薪收入高于5万的人数记为ξ,求ξ的分布列和期望;
(3)已知员工年薪收入与工作年限成正线性相关关系,若某员工工作第一年至第四年的年薪分别为3万元、4.2万元、5.6万元、7.2万元,预测该员工第五年的年薪为多少?
附:线性回归方程$\hat y=\hat bx+\hat a$中系数计算公式:$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{{{(\;{x_i}-\overline x\;)}^2}}}$,$\hat a=\overline y-\hat b\;\overline x$,其中$\overline x$、$\overline y$表示样本均值.
分析 (1)根据表格数据计算;
(2)适用组合数公式计算P(ξ);
(3)求出线性回归方程,根据回归方程预测.
解答 解:(1)平均值为10万元,中位数为6万元.
(2)年薪高于5万的有6人,低于或等于5万的有4人;ξ的取值为0,1,2.P(ξ=0)$\frac{{C}_{4}^{2}}{{C}_{10}^{2}}$=$\frac{2}{15}$,$P(ξ=1)=\frac{C_4^1C_6^1}{{C_{10}^2}}=\frac{8}{15}$,$P(ξ=2)=\frac{C_6^2}{{C_{10}^2}}=\frac{1}{3}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | $\frac{2}{15}$ | $\frac{8}{15}$ | $\frac{1}{3}$ |
(3)设xi,yi(i=1,2,3,4)分别表示工作年限及相应年薪,则$\overline{x}=2.5,\overline{y}=5$,
$\sum_{i=1}^{4}({x}_{i}-\overline{x})^{2}$=2.25+0.25+0.25+2.25=5,$\sum_{i=1}^4{({x_i}-\overline x)({y_i}-\bar y)}=-1.5×(-2)+(-0.5)×(-0.8)+0.5×0.6+1.5×2.2=7$,
∴$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{{{(\;{x_i}-\overline x\;)}^2}}}$=1.4,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=5-1.4×2.5=1.5.
∴员工年薪与工作年限的线性回归方程为$\stackrel{∧}{y}$=1.4x+1.5.
当x=5时,$\stackrel{∧}{y}$=1.4×5+1.5=8.5.
该员工第5年的年薪收入约为8.5万元.
点评 本题考查了古典概型的概率计算,线性回归方程的解法及应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知集合B={1},A∪B={1,2},则A=( )
| A. | ∅ | B. | {2} | C. | {1,2} | D. | {2}或{1,2} |
20.已知直线l的方程为ax+2y-3=0,且a∈[-5,4],则直线l的斜率不小于1的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{7}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
10.已知直线l:kx+y-2=0(k∈R)是圆C:x2+y2-6x+2y+9=0的对称轴,过点A(0,k)作圆C的一条切线,切点为B,则线段AB的长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
17.一个几何体的三视图如图所示,则该几何体的体积是( )
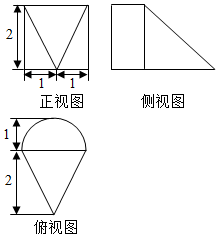

| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |
 如图,正方体ABCD-A1B1C1D1中,P是AD的中点.
如图,正方体ABCD-A1B1C1D1中,P是AD的中点.