题目内容
6.在空间中,设m,n为两条不同直线,α,β为两个不同平面,则下列命题正确的是( )| A. | 若m∥α且α∥β,则m∥β | |
| B. | 若α⊥β,m?α,n?β,则m⊥n | |
| C. | 若m⊥α且α∥β,则m⊥β | |
| D. | 若m不垂直于α,且n?α,则m必不垂直于n |
分析 在A中,m∥β或m?β;在B中,m与n相交、平行或异面;在C中,由线面垂直的判定定理得m⊥β;在D中,m有可能垂直于n.
解答 解:由m,n为两条不同直线,α,β为两个不同平面,知:
在A中,若m∥α且α∥β,则m∥β或m?β,故A错误;
在B中,若α⊥β,m?α,n?β,则m与n相交、平行或异面,故B错误;
在C中,若m⊥α且α∥β,则由线面垂直的判定定理得m⊥β,故C正确;
在D中,若m不垂直于α,且n?α,则m有可能垂直于n,故D错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
16.已知集合B={1},A∪B={1,2},则A=( )
| A. | ∅ | B. | {2} | C. | {1,2} | D. | {2}或{1,2} |
17.一个几何体的三视图如图所示,则该几何体的体积是( )
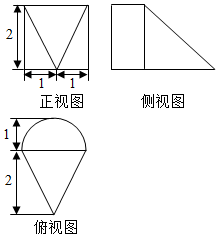

| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |
1. 如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
 如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )
如图是底面半径为1,高为2的圆柱被削掉一部分后剩余的几何体的三视图(注:正视图也称主视图,侧视图也称左视图),则被削掉的那部分的体积为( )| A. | $\frac{π+2}{3}$ | B. | $\frac{5π-2}{3}$ | C. | $\frac{5π}{3}$-2 | D. | 2$π-\frac{2}{3}$ |
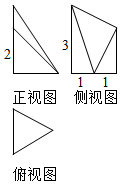 某多面体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角梯形,则该多面体的表面积为10+$\sqrt{3}$+$\sqrt{10}$,体积为$\frac{5\sqrt{3}}{3}$.
某多面体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角梯形,则该多面体的表面积为10+$\sqrt{3}$+$\sqrt{10}$,体积为$\frac{5\sqrt{3}}{3}$.