题目内容
2.记定义在区间[a,b]上的连续函数y=f(x),如果存在x0∈[a,b],使得f(x0)=$\frac{{∫}_{a}^{b}f(x)dx}{b-a}$成立,则称x0为函数f(x)在[a,b]上的“平均值点”,那么函数f(x)=x3+2x在[-1,1]上“平均值点”的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由新定义计算定积分可将问题转化为g(x)=x3+2x-$\frac{5}{4}$在x∈[-1,1]上的零点个数,由零点判定定理和函数单调性可得.
解答 解:由题意可得${∫}_{-1}^{1}$(x3+2x)dx=($\frac{1}{4}$x4+x2)${|}_{-1}^{1}$=0,
∴函数f(x)=x3+2x在[-1,1]上“平均值点”的个数为方程x3+2x=0在[-1,1]上根的个数,
构造函数g(x)=x3+2x,则问题转化为g(x)在x∈[-1,1]上的零点个数,
求导数可得g′(x)=3x2+2>0,故函数g(x)在x∈[-1,1]上单调递增,
由g(-1)g(1)<0,故函数g(x)在x∈[-1,1]上有唯一一个零点.
故选:A.
点评 本题考查定积分的运算,涉及转化和数形结合的思想,属中档题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
17.设函数y=log2$\frac{3}{x-1}$的定义域为集合A,函数y=$\root{3}{x-2}$的定义域为集合B,则A∩B为( )
| A. | {x|x≥2} | B. | {x|x≠1} | C. | {x|x>2} | D. | {x|x>1} |
10.已知直线l:kx+y-2=0(k∈R)是圆C:x2+y2-6x+2y+9=0的对称轴,过点A(0,k)作圆C的一条切线,切点为B,则线段AB的长为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
17.一个几何体的三视图如图所示,则该几何体的体积是( )
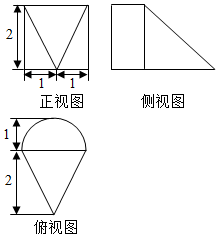

| A. | $π+\frac{8}{3}$ | B. | $\frac{π}{3}+\frac{8}{3}$ | C. | π+8 | D. | $\frac{π}{2}+\frac{8}{3}$ |
 如图,正方体ABCD-A1B1C1D1中,P是AD的中点.
如图,正方体ABCD-A1B1C1D1中,P是AD的中点.