题目内容
16.若三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,则实数x的值为( )| A. | 10 | B. | -10 | C. | 5 | D. | -5 |
分析 三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,可得kAB=kAC,即可得出.
解答 解:三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,
∴kAB=kAC,∴$\frac{-2-8}{-1-4}$=$\frac{-2-x}{-1-5}$,
解得x=10.
故选:A.
点评 本题考查了三点共线与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.向量$\overrightarrow a=({2,-1}),\overrightarrow b=({x,1})$,若$2\overrightarrow a+\overrightarrow b$与$\overrightarrow b$共线,则x=( )
| A. | 2 | B. | -2 | C. | $-2+\sqrt{5}$ | D. | $-2-\sqrt{5}$ |
1.定义在(-∞,0)上的可导函数f(x)的导数为f'(x),且有xf'(x)-2f(x)>x2,若f(m+2015)-(m+2015)2f(-1)>0,则实数m的取值范围是( )
| A. | (-2016,0) | B. | (-∞,-2017) | C. | (-∞,-2016) | D. | (-2016,-2015) |
3.若函数f(x)=xex-m在R上存在两个不同的零点,则m的取值范围是( )
| A. | m>e | B. | m>-$\frac{1}{e}$ | C. | -$\frac{1}{e}$<m<0 | D. | -e<m<0 |
 用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行的第二个数为bn(n≥2).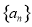 的前
的前 项和为
项和为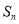 ,且
,且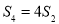 ,
,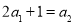 .
.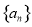 的通项公式;
的通项公式;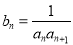 ,求
,求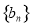 的前
的前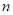 项和
项和 .
.