题目内容
1.定义在(-∞,0)上的可导函数f(x)的导数为f'(x),且有xf'(x)-2f(x)>x2,若f(m+2015)-(m+2015)2f(-1)>0,则实数m的取值范围是( )| A. | (-2016,0) | B. | (-∞,-2017) | C. | (-∞,-2016) | D. | (-2016,-2015) |
分析 对不等式xf′(x)-2f(x)>x2两边同除以-x3便可据条件得出$(\frac{f(x)}{{x}^{2}})′>0$,从而判断出函数F(x)=$\frac{f(x)}{{x}^{2}}$在(-∞,0)上单调递增,这样可由不等式f(m+2015)-(m+2015)2f(-1)>0得出F(m+2015)>F(-1),这样根据F(x)的定义域及单调性即可求出m的取值范围.
解答 解:由xf′(x)-2f(x)>x2(x<0)得,
$\frac{xf′(x)-2f(x)}{-{x}^{3}}>-\frac{1}{x}>0$;
∴$(\frac{f(x)}{{x}^{2}})′>0$;
设F(x)=$\frac{f(x)}{{x}^{2}}$,则F(x)在(-∞,0)上单调递增;
由f(m+2015)-(m+2015)2f(-1)>0得,$\frac{f(m+2015)}{(m+2015)^{2}}>f(-1)$;
即$\frac{f(m+2015)}{(m+2015)^{2}}>\frac{f(-1)}{(-1)^{2}}$;
∴F(m+2015)>F(-1);
∴-1<m+2015<0;
∴-2016<m<-2015;
∴m的取值范围是(-2016,-2015).
故选D.
点评 考查通过构造函数解决函数问题的方法,以及函数导数符号和函数单调性的关系,商的导数的计算公式,以及不等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,则实数x的值为( )
| A. | 10 | B. | -10 | C. | 5 | D. | -5 |
9.在一次期末数学测试中,唐老师任教班级学生的考试得分情况如表所示:
(1)根据上述表格,试估计唐老师所任教班级的学生在本次期末数学测试的平均成绩;
(2)若学生的成绩大于或等于130分为优秀,小于130分且大于等于90分为合格,小于90分为不及格,若是优秀,学生在期末综合测评中可得到40分,若是合格,学生在期末综合测评中可得到20分,若是不合格,学生在期末综合测评中则扣20分,以频率估计概率,若从大量的学生中随机抽取2人,这2人在数学科目的期末综合测评分数之和记为X,求X的分布列和数学期望.
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
(2)若学生的成绩大于或等于130分为优秀,小于130分且大于等于90分为合格,小于90分为不及格,若是优秀,学生在期末综合测评中可得到40分,若是合格,学生在期末综合测评中可得到20分,若是不合格,学生在期末综合测评中则扣20分,以频率估计概率,若从大量的学生中随机抽取2人,这2人在数学科目的期末综合测评分数之和记为X,求X的分布列和数学期望.
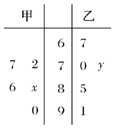 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);