题目内容
7.${({\sqrt{x}+\frac{2}{x^2}})^n}$展开式中只有第六项二项式系数最大,则n=10,展开式中的常数项是180.分析 由${({\sqrt{x}+\frac{2}{x^2}})^n}$展开式中只有第六项二项式系数最大,可得n=10.再利用$(\sqrt{x}+\frac{2}{{x}^{2}})^{10}$的通项公式即可得出.
解答 解:∵${({\sqrt{x}+\frac{2}{x^2}})^n}$展开式中只有第六项二项式系数最大,∴n=10.
∴$(\sqrt{x}+\frac{2}{{x}^{2}})^{10}$的通项公式:Tr+1=${∁}_{10}^{r}$$(\sqrt{x})^{10-r}(\frac{2}{{x}^{2}})^{r}$=2r${∁}_{10}^{r}$${x}^{5-\frac{5r}{2}}$,解得r=2.
∴常数项为:${2}^{2}{∁}_{10}^{2}$=180.
故答案为:10,180.
点评 本题参考二项式定理的展开式及其通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
20.在下列函数中,当x取正数时,最小值为2的是( )
| A. | $y=x+\frac{4}{x}$ | B. | $y=lg(x+1)+\frac{1}{lg(x+1)}$ | ||
| C. | $y=\sqrt{{x^2}+1}+\frac{1}{{\sqrt{{x^2}+1}}}$ | D. | $y=sinx+\frac{1}{sinx},({0<x<\frac{π}{2}})$ |
2.已知集合U=R,集合A={x|2x>1},集合B={x|logx2>0},则A∩(∁UB)等于( )
| A. | {x|x>1} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|x≤1} |
16.若三点A(-1,-2),B(4,8),C(5,x)在同一条直线上,则实数x的值为( )
| A. | 10 | B. | -10 | C. | 5 | D. | -5 |
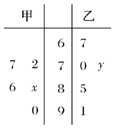 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);