题目内容
10.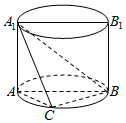 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.(1)求证:平面AA1C⊥平面BA1C;
(2)若AC=BC,求几何体A1-ABC的体积V.
分析 (1)证明BC⊥平面AA1C,即可证明平面AA1C⊥平面BA1C;
(2)求出AC,直接利用体积公式求解即可.
解答 (1)证明:因为C是底面圆周上异于A,B的一点,AB是底面圆的直径,
所以AC⊥BC.
因为AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC,
而AC∩AA1=A,所以BC⊥平面AA1C.
又BC?平面BA1C,所以平面AA1C⊥平面BA1C.…(6分)
(2)解:在Rt△ABC中,AB=2,则由AB2=AC2+BC2且AC=BC,
得$AC=BC=\sqrt{2}$,
所以${V_{{A_1}-ABC}}=\frac{1}{3}{S_{△ABC}}•A{A_1}=\frac{1}{3}•\frac{1}{2}•\sqrt{2}•\sqrt{2}•2=\frac{2}{3}$.…(12分)
点评 本题考查线面垂直的判定,考查平面与平面垂直,考查几何体A1-ABC的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{{4}^{x},x>0}\\{f(x+1)-1,x<0}\end{array}\right.$,则f(-$\frac{1}{2}$)+f($\frac{1}{2}$)=( )
| A. | 3 | B. | 5 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
5.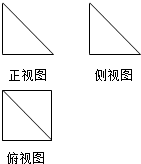 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
15.已知单位向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,则函数f(x)=(x$\overrightarrow{a}$+$\overrightarrow{b}$)2 (x∈R)( )
| A. | 既不是奇函数也不是偶函数 | B. | 既是奇函数又是偶函数 | ||
| C. | 是偶函数 | D. | 是奇函数 |
20.在△ABC中,已知a=1,b=$\sqrt{3}$,A=120°,则此三角形( )
| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 解的个数不确定 |