题目内容
20.在△ABC中,已知a=1,b=$\sqrt{3}$,A=120°,则此三角形( )| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 解的个数不确定 |
分析 由已知数据和正弦定理可得sinB=$\frac{3}{2}$>1,矛盾,可得无解.
解答 解:∵在△ABC中a=1,b=$\sqrt{3}$,A=120°,
∴由正弦定理可得sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×\frac{\sqrt{3}}{2}}{1}$=$\frac{3}{2}$>1,
∴此三角形无解,
故选:A.
点评 本题考查三角形解的个数的判定,属基础题.

练习册系列答案
相关题目
11.设f(x)=3x+3-x,则f(x)是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
12.在正项等比数列{an}中,若1og2(a1a2a3…a9)=18,且a2,a4是方程x2+mx+4=0的两根,则数列{an}的通项公式为( )
| A. | 2${\;}^{-\frac{n-3}{2}}$ | B. | 2${\;}^{\frac{n-3}{2}}$ | C. | 2${\;}^{\frac{n-1}{2}}$ | D. | 2${\;}^{\frac{n}{2}}$ |
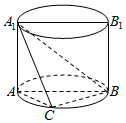 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2. 如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.
如图所示,AB为半圆ACB的水平直径,C为圆上的最低点,一小球从A点以速度v0被水平抛出后恰好落在C点,设重力加速度为g,不计空气阻力,求圆的半径.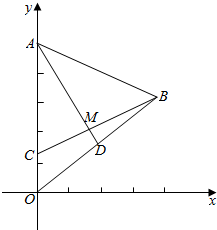 如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标.
如图所示,已知△AOB中,A(0,5),O(0,0),B(4,3),$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$,$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$,AD与BC相交于点M,求点M的坐标.