题目内容
1.已知函数$f(x)={sin^2}ωx+\sqrt{3}sinωx•sin(\frac{π}{2}+ωx)$,(ω>0)的最小正周期是π,则ω=1,f(x)在$[\frac{π}{4},\;\frac{π}{2}]$上的最小值是1.分析 由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(2ωx-$\frac{π}{6}$)+$\frac{1}{2}$,结合ω>0,由周期公式即可解得ω的值,从而解得f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,由正弦函数的单调性可得f(x)在$[\frac{π}{4},\;\frac{π}{2}]$上的最小值.
解答 解:∵f(x)=sin2ωx+$\sqrt{3}$sinωxsin(ωx+$\frac{π}{2}$)
=$\frac{1-cos2ωx}{2}$+$\sqrt{3}$sinωxcosωx
=sin(2ωx-$\frac{π}{6}$)+$\frac{1}{2}$,
∴由ω>0,π=$\frac{2π}{2ω}$,可解得:ω=1.
∴可得f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,
∵x∈$[\frac{π}{4},\;\frac{π}{2}]$,可得:2x-$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],
∴f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$∈[1,$\frac{3}{2}$],
∴f(x)在$[\frac{π}{4},\;\frac{π}{2}]$上的最小值是1.
故答案为:1,1;
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
13.命题“?x∈R,x2-5x+1>0”的否定为( )
| A. | ?x∈R,x2-5x+1≤0 | B. | ?x∈R,x2-5x+1≤0 | C. | ?x∈R,x2-5x+1<0 | D. | ?x∈R,x2-5x+1>0 |
11.设f(x)=3x+3-x,则f(x)是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
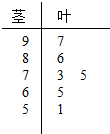 北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩.
北京高中会考考试科目原始得分采用百分制,公布成绩使用A、B、C、D等级制.A、B、C三级为合格等级,D为不合格等级.各等级分数划分标准:85分及以上为A,84-70分为B,69-60分为C,60分以下为D.如图的茎叶图(十位为茎,个位为叶)记录了某校高三年级6名学生的数学会考成绩. 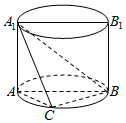 如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.
如图,AA1B1B是圆柱的轴截面,C是底面圆周上异于A,B的一点,AA1=AB=2.