题目内容
15．已知单位向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$，则函数f（x）=（x$\overrightarrow{a}$+$\overrightarrow{b}$）2 （x∈R）（ ）| A． | 既不是奇函数也不是偶函数 | B． | 既是奇函数又是偶函数 | ||
| C． | 是偶函数 | D． | 是奇函数 |
分析 由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=0，函数f（x）=（x$\overrightarrow{a}$+$\overrightarrow{b}$）2 =x2+1，由此可得函数的奇偶性．
解答 解：由题意可得$\overrightarrow{a}$•$\overrightarrow{b}$=0，|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，
∴函数f（x）=（x$\overrightarrow{a}$+$\overrightarrow{b}$）2 =x2+2$\overrightarrow{a}$•$\overrightarrow{b}$x+1=x2+1，
显然，函数f（x）为偶函数，
故选C．
点评 本题主要考查两个向量垂直的性质，函数的奇偶性的判断，属于中档题．
练习册系列答案
相关题目
3．命题p：?α∈R，cos（π+α）=cosα，命题q：?x∈R，x2+1＞0，则下面结论正确的是（ ）
| A． | p是假命题 | B． | ￢q是真命题 | C． | p∨q是假命题 | D． | p∨q是真命题 |
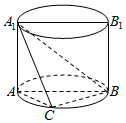如图，AA1B1B是圆柱的轴截面，C是底面圆周上异于A，B的一点，AA1=AB=2．